I was solving this particular problem Array transformer Here N=300000 and Q=50000,for a block size of 600 i got a run time of 1.2sec and it decreased as I increased block size to around 2000..it was nearly 0.620 sec. But shouldn't the optimal value be at sqrt(300000)==550??
→ Обратите внимание
До соревнования
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
5 дней
Зарегистрироваться »
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
5 дней
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 156 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | nor | 152 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 25.11.2024 16:40:00 (h1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|










When you set the blocks size 2000 your program works fast if it gets input data of that test cases, but in general it works slower then the original algorithm. As test cases for that problems are set in advance your program worked fast by chance. If you sent the solution at a CodeForces contest, somebody would hack you. And yes, optimal size of blocks in SQRTdecomposition is sqrt(N).
I think it should depend on the operation you are going to perform in your algorithm, sometimes having more groups than exactly can lead to a faster solution due to constant factors, but it could also be the other way around.
can lead to a faster solution due to constant factors, but it could also be the other way around.
But is there any way we can find that optimal block size??
I would just write down the time complexity with the variable K as block size, and then find the minima of the function by computing the derivation and setting it 0.
E.g. if the complexity is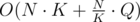 with N ≈ Q, then we have the derivation
with N ≈ Q, then we have the derivation 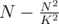 . We get the minimum by setting it zero:
. We get the minimum by setting it zero: 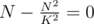 , which gives
, which gives 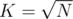 after some transformations.
after some transformations.
Now I don't know exactly how you solved the problem. I'm guessing by keeping a sorted version of each block in memory, so that you can answer a question in each block with a binary search. That way you initially need to sort each block first, however this doesn't influence the complexity much. Then to answer a query you need to to at most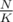 binary searches and iterate twice over complete blocks:
binary searches and iterate twice over complete blocks: 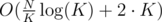 and updating a block can be done in O(K) time.
and updating a block can be done in O(K) time.
This gives the total complexity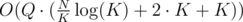 time. Computing the minimum can be a bit painful, so I just computed it with WolframAlpha. It suggests that the actual best value for K is 916.
time. Computing the minimum can be a bit painful, so I just computed it with WolframAlpha. It suggests that the actual best value for K is 916.
Obviously you still should take these results with caution, as this is only a theoretical guess. (In the same way as two function with the same complexity can have a pretty different runtime because of the hidden factors.) In the end it still boils down to experience and timing the solutions with a few examples.
It depends on the code (things like how cache friendly it is, the operations it uses, how loop-unrolling friendly it is, how branch-prediction friendly it is). For problems that you use O(number of blocks * N) memory you can almost always assume that you should use a bit less blocks because of cache misses (it uses less memory so there are more cache hits). Some problems also have the optimal point in sqrt(nlogn) or sqrt(n/logn), to find that you just need to learn to optimize a function. If it's just 2 terms and one increases/the other decreases you can almost always just assume that they will be equal to find the order of the best choice too (N^2 / M = N * M, M = sqrt(N))