| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
In this post I introduce the existence of https://beta.atcoder.jp/. It's a bit more advanced than atcoder.jp, and usually it's also faster to load.
This is an example of beta version of contest page (tomorrow's ARC). For example you can filter your friends in the standings. Please use it!
Thanks for creating such awesome platform and Quality problems
Thanks for posting it here, I've updated Competitive Companion to work with the beta platform aswell.
do we have to update as well
If you installed it via Firefox' AMO or Chrome's Web Store, it will automatically update somewhere in the next 5-24 hours (Chrome checks for updates every 5 hours, Firefox every 24 hours).
If you installed manually by downloading the packaged zip from GitHub and unpacking it in your browser, you would probably not be asking this question, but then you obviously also need to update manually.
Thanks for creating such awesome plugin really helpfull for java users
I think beta is available for quite a while. Is there a reason why it doesn't replace old site?
I know the reason. There are some contests for some companies' recruitment. It's usually for Japanese. For participating this type of contests, it needs application forms (ex. real name, where are you live, when are you going to graduate). The reason for not replacing old site is, the forms are not supported in beta version.
Could you please make announcements when rounds are rescheduled at unusual time?
It was clearly mentioned in the email invitation that it starts 30 minutes earlier. Quoting from the email : "Time: July 1st (Sunday), 20:30 JST (This is 30 minutes earlier than usual.)" ..
Who cares about email invitations?
For Problem Linear Approximation, I was using ternary search approach to find answer. At start of contest, My low and high limits were -2e18 and 2e18 respectively. Constantly, I was getting WA. At the last minute of contest, I changed limits of low = -1e10 and high = 1e10, and don't know what but it got accepted.
Can anyone check this codes and tell why Code1 gets WA and Code2 gets AC ?
Code1, getting WA
Code2, getting AC
When low and high are about 1018 your code will overflows.
Thanks for quick reply, I should have taken care of such a silly mistake!!
You could have used simple binary search. I felt binary was more intuitive. Also since range of elements was from 1 to 1e9 so checking for b in range outside [-1e9,1e9] won't help. Check this if interested : Link
I used ternary by comparing f(mid-1) and f(mid). In a way, it's a binary search, Code!
The editorial to the problem Linear approximation states:
This is because, if b is not the median, if we continuously change b to the direction of the median, the sum of abs(Bi−b) never increases.
How can we show that?
Firstly, decrease each Ai by i. The problem is equivalent to find minimum value of
S = |A1 - b| + |A2 - b| + ... |An - b|
Using the triangle inequality, S ≥ |A1 + A2 + ... + An - n·b|. Let's divide it into two cases, A1 + A2 + ... + An - n·b ≥ 0 and vice versa. In the first case, we get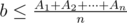
and we want larger b. In the latter case we get 
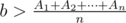and we want smaller b. So with checking two values of b is enough to solve the problem.