Hello, Codeforces!
We're glad to have ko_osaga as a problem setter!
We're going to host a new contest at csacademy.com. Round #84 will take place on Wednesday, July 18th, 15:05:00 UTC. This contest will be a Div1 + Div2, with 7 tasks of varying difficulty that need to be solved in 2 hours.
Facebook event
We recently created a new Facebook event. If you choose "Interested" here, you will be notified before each round we organise from now on.
Contest format:
- You will have to solve 7 tasks in 2 hours.
- There will be full feedback throughout the entire contest.
- Tasks will not have partial scoring, so you need to pass all test cases for a solution to count (ACM-ICPC-style).
- Tasks will have dynamic scores. According to the number of users that solve a problem the score will vary between 100 and 1000.
- Besides the score, each user will also get a penalty that is going to be used as a tie breaker.
Prizes
We're going to award the following prizes:
- First place: 100$
- Second place: 50$
About the penalty system:
- Computed using the following formula: the minute of the last accepted solution + the penalty for each solved task. The penalty for a solved task is equal to log2 (no_of_submissions) * 5.
- Solutions that don't compile or don't pass the example test cases are ignored.
- Once you solve a task you can still resubmit. All the following solutions will be ignored for both the score and the penalty.
If you find any bugs please email us at [email protected]
Don't forget to like us on Facebook, VK and follow us on Twitter.











Oh my god... it is Koosaga round??????
From what I know, yes. I think it'll be cool tbh
omg alex.velea why are you doing this to me
Hopefully there will be a Div.1 settled by alex.velea in the future as well.
How to solve D?
I got a pretty overkill-ish solution.
Let's iterate over each x from the input and check the answer in point (x, 0). You can show that the minimal answer will always be in some of them.
Sort points by x.
Maintain a set of values L points to the left (or equal to x) of the current x add. They add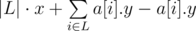 to the answer. Points to the right of x will be stored in some structure that can remove elements and get the sum of the k minimal ones by comparator (x + y) (because the answer for that structure is the sum of these values minus (k - |L|)·x) (I did it with compressing these values and having a segment tree with 1s and 0s and BIT for sums). Now when transitioning to the next x, you remove the corresponding points from the structure and add them to set. Now you remove points from the set (by the greatest value) until its size is k or smaller. Finally, you remove the greatest values from the set if it's making the answer smaller (check for the current answer and for the answer withoit the greatest element of L and with k - |L| + 1 elements from the structure).
to the answer. Points to the right of x will be stored in some structure that can remove elements and get the sum of the k minimal ones by comparator (x + y) (because the answer for that structure is the sum of these values minus (k - |L|)·x) (I did it with compressing these values and having a segment tree with 1s and 0s and BIT for sums). Now when transitioning to the next x, you remove the corresponding points from the structure and add them to set. Now you remove points from the set (by the greatest value) until its size is k or smaller. Finally, you remove the greatest values from the set if it's making the answer smaller (check for the current answer and for the answer withoit the greatest element of L and with k - |L| + 1 elements from the structure).
You can just erase from |L| because these points will never be needed anyway.
Code
So... did anyone else solve E and then realized the same solution applies to D in O(nlog^2n) with fenwick + binary search?
Editorial is finally live. Sorry for being very late!
We first observe that the diameter of tree can be calculated in linear time. There exists two well-known method for this : One being the algorithm that picks two farthest point, and another being DP on tree. However, the first algorithm doesn't work on trees with with negative edge weight! Thus, you should use DP in this problem. This one trapped a lot of contestant, so let's take this as a valuable lesson!
For this problem, weight of every edge is a linear function on k. As distance is a sum of weight over every edge in path, it is also a linear function on k. Thus, for fixed date D, our problem is about finding maximum y-intercept with x = D, from a lot of linear functions.
We have a lot of linear functions (O(n2)!), and they don't share a good property from the first observation, so this may not sound like a good approach. However, this approach gives another nice observation : If you draw some bunch of lines in the paper, you can notice that maximum y-intercept is a convex function. Thus, the diameter is also a convex function with respect to date D. We will denote it as f(D) for convenience.
How to find a minimum in a convex function f ? Well-known method like ternary search should work, but we can make it simpler as the domain of function is integer. Convex function has a monotonically increasing derivative, so you can just find a first position where it's derivative hits zero. Formally, you can find minimum x such that f(x + 1) - f(x) ≥ 0. This can be done with binary search.
Total time complexity is O(NlgD), but there is a huge cache miss if implemented naively. This is why we had 8s time limit.
We first start by discussing the case N = 2, which is basically the time when two growing squares meet. When we draw a bounding rectangle for the center cell, then we get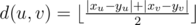 , which is a manhattan distance between two center cells, divided by 2.
, which is a manhattan distance between two center cells, divided by 2.
Then, how will the generalization work? We can imagine d(u, v) as a day that city u and city v merges — after that day you can move between u and v with only developed cells. Then, f(u, v) is the first day where u and v belongs to the same component.
How can we find a single f(u, v) efficiently? Note that there is no more than n - 1 important events for merging — most of them are useless as they don't change the components. If we dig more, we can observe that those important events are actually the edges in minimum spanning tree, where the graph is complete and two vertex u and v is connected with edge cost d(u, v). Then, we can find a maximum cost edge along the path u - v in MST to calculate f(u, v).
With the MST, we can also calculate the sum : Instead of iterating through pairs, we iterate through the edges, and calculate the number of pairs that have the maximum as this edge. If we sort the edges of tree in increasing order (e1, e2, ..., en - 1) , this corresponds to a number of pair that wasn't connected with edges e1, ... ei - 1, but that was connected with edges e1, ..., ei. This can be calculated with disjoint set with sizes in each component, as the number of pair will be same with the product of each two component that edges merge.
Now, we are left with finding a MST for a complete graph, where the weight function is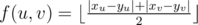 . Note that, if we set f(u, v) = |xu - yu| + |xv - yv| and calculate its minimum spanning tree, then that tree also optimizes
. Note that, if we set f(u, v) = |xu - yu| + |xv - yv| and calculate its minimum spanning tree, then that tree also optimizes 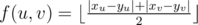 — this can be easily proved if you imagine how Kruskal algorithm works. Thus, it would be better to use taxicab metric here.
— this can be easily proved if you imagine how Kruskal algorithm works. Thus, it would be better to use taxicab metric here.
An algorithm for Taxicab metric MST is discussed in a Topcoder article, and the whole algorithm relies on this simple and beautiful lemma.
It can be proved by standard proof-by-contradiction, which I encourage you to try by yourself. (You have the Topcoder article, if you are stuck...)
Now, the problem is reduced into finding closest point in each octant. WLOG we can consider only one octant, as the other can be easily constructed by symmetry on x = y, x = 0, y = 0. If we consider the northeast — east octant, we have to calculate the point with minimum xj + yj, where yj > yi, xj - yj ≥ xi - yi (watch out for the equality!)
This is a good exercise on line sweep : If we sweep through y coordinate, and make a range minimum query for a tree with key x - y, the whole problem can be solved in . After then, we have to run Kruskal's algorithm on at most 8n edges, to calculate the MST (and simulatenously calculate the sum, without any extra steps).
. After then, we have to run Kruskal's algorithm on at most 8n edges, to calculate the MST (and simulatenously calculate the sum, without any extra steps).
Seokhwan's First Day : Persistent Segment Tree
Left-to-right sweep from 1 to M is a tempting approach for this problem, as we can regard each update as range queries. However, it's surprisingly hard to proceed further this way — comparison queries are online, and it's hard to make any kind of precomputation for them.
However, you can actually store all the vectors with persistent data structure (which we'll assume that you know). We make a persistent segment tree, which have its values on the leaf. WLOG assume M = 218. Then we can let auxiliary vector V0 as an empty binary tree with value 0 on leaf.
We now proceed inductively, from Vi - 1 to Vi. As the queries are affecting a vectors in an interval, each query make two difference in the element of vectors — we change A[p] = v starting from Vs, and A[p] = 0 starting from Ve + 1. As we want to save all the vectors without harming others, we make new leaf nodes, and O(lgN) auxiliary nodes in each updates. With this method, we can build the whole N binary tree in O(QlgM) time and space complexity.
Seokhwan's Second Day : Sorting by each level
If we sort the binary trees naively, we will definitely need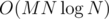 time, as the comparison function should search the trees with DFS.
time, as the comparison function should search the trees with DFS.
However, this followiing idea can optimize the above algorithm : We first start by the grid with 2k-length vectors, and we halve the length of vectors for each iteration. This can be done by coordinate compression — we collect all the pair (A[1], A[2]), (A[3], A[4]), ..., (A[2k - 1], A[2k]), sort by lexicographical order, and replace it with a single number that can express it's relative order. If we repeat this for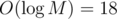 times, we can find a final sorted order!
times, we can find a final sorted order!
Maybe this doesn't sound like a good approach, as the grid is very large. But, remember that every such interval corresponds to a node in a persistent segment tree, which means that we know there is at most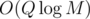 such things, in particular, O(Q) nodes for each level. Thus, a simple
such things, in particular, O(Q) nodes for each level. Thus, a simple 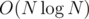 sorting and coordinate compression algorithm suffices for
sorting and coordinate compression algorithm suffices for 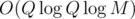 algorithm.
algorithm.
At the very last, this can be optimized to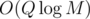 by replacing
by replacing 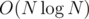 sorting to O(N) counting sort — as counting sort is a stable sort, simply sorting through second argument and then first argument would work. However, this optimization doesn't give a significant performance boost, and the
sorting to O(N) counting sort — as counting sort is a stable sort, simply sorting through second argument and then first argument would work. However, this optimization doesn't give a significant performance boost, and the 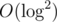 solution will be enough fast for getting AC.
solution will be enough fast for getting AC.
As a side note, this part closely resembles the Manber-Myers suffix array algorithm. It increases the scope of comparison each time, and it utilizes counting sort to get rid of it's log factor.
suffix array algorithm. It increases the scope of comparison each time, and it utilizes counting sort to get rid of it's log factor.
Huge thanks to CSA team for their amazing platform and helps, and tester khsoo01!