→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
20:03:11
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
20:03:11
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 21:31:51 (i1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











Как решать 500? Написал тупую динамику без всяких отсечений, её, разумеется, сломали (правда, с третьей попытки).
Я перебирал циклический сдвиг. Дальше решал задачу для отрезка динамикой z[i][j] — где стоим и сколько должны начиная с нашей позиции выкинуть.
Сколько выкинуть же всегда определено уровнем карты?
У нас могут быть открыты несколько карт.
Посмотрим на итоговый ответ. Понятно, что в нём будет такое i, что среди i + 1, ..., i + li - 1 нет взятых в ответ элементов (в начальной конфигурации; просто возьмём какой-то элемент и пойдём от него направо, пока не упрёмся в требуемый, круг мы сделать не можем). А значит, перебираем элемент-"разрез" и проходимся тупой динамикой с конца разрезанного круга.
не очень понятно, что за тупая динамика?
Ну d[i][j] — мы находимся на i'ом с конца элементе и у нас "в запасе" есть j элементов для удаления; переходы — либо i + 1, j + 1, либо i + 1, j + 1 - li с увеличением урона на d[i]. Но если немного подумать, эта динамика упрощается до выбора элементов с суммой li не больше n, как пишут ниже; т.к. любое такое подмножество можно набрать, пройдя справа налево.
Можно просто выбирать набор карточек с сумой уровней не больше n, c максимальным уроном.
Рюкзак, где вес вещи — li, а стоимость — di. Нужно набрать вещей с суммарным весом не более N.
У меня в комнате один из участников посабмитил по easy перебор. Я долго думал как его почеленджить так и не понял. Passed system tests.
Это странное чувство, когда на вторую задачу уходит меньше времени, чем на первую...
У меня другое чувство, когда на третью уходит меньше времени, чем на вторую :(
UPD: А потом еще другое чувство, когда видишь решение в две строчки по 500
А как решать 950?
Расскажу свое решение, не претендую на оптимальность асимптотики и времени написание кода. :) Придумал на раунде, но написать не успел и досдал только что в практисе.
Рассмотрим нашу решетку как детерминированный конечный автомат над алфавитом {L, R, U, D}. Состояниями будут вершины сетки, в которых нет препятствия, а также будет сток, который будет допускающим состоянием. Переходы из состояния по каждой букве ведут в ту вершину, куда сместилась бы монетка на этой позиции при заданном действии. Если она падает со стола, направим ребро в сток.
Когда положение монет хорошее? Когда есть 2 монеты, которые лежат на неэквивалентных состояниях (ибо есть различающая их строка, а значит, одна упадет, а другая -- нет). Посчитаем, сколько таких расстановок (точнее, посчитаем все и вычтем плохие). Плохие — это когда монетки лежат на позициях, соответствующих эквивалентным состояниям. Вычтем в таком случае из ответа 2cnt - 1, где cnt -- количество вершин в каком-то классе эквивалентности. Итого,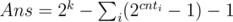 , где cnti — количество вершин в i классе эквивалентности вершин в автомате, и
, где cnti — количество вершин в i классе эквивалентности вершин в автомате, и 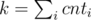 .
.