tatya_bichu's blog

Find minimum steps to reduce to one
By tatya_bichu, history, 6 years ago, In English

Given T test cases T<=100000 In each test case given a positive integer A.A<=100000 You can perform any of the following steps(one of them):.

1) decrement A by 1.

2) increment A by 1.

3) divide A by one of it's prime factor.

Find minimum number of steps to reduce A to 1. 1) it is best to divide by max prime factor or finding nearest prime number whichever is minimum. This is codeforces problem but I can't find it

  • Vote: I like it
  • +4
  • Vote: I do not like it

Comments Comments (21)
| Write comment?
»
6 years ago, # |
  Vote: I like it +4 Vote: I do not like it

Constraints of A?

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

if increment by 1 step would not be there then it can be done in aloga time..by maintaining the lowest prime divisor for each numbers(1->a) using seive then maintaining the answer(dynamic programming) array of size (a+1) using indices (1->a), ans[1]=0 and ans[i] can be calculated by min(ans[i-1],min(ans[i/p] for all prime divisors of i )) + 1. prime divisors for a particular number 'n' can be found in logn time hence it is (seive + aloga).. pls somebody explain how to do this with increment operation also

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Basically you can return 1 for each prime number and the prime gap at most can be around 100 so algo:

    Int solve(a){ If(a==1). Return 0;

    If(isprime[a]) return 1;

    Return min(solve (a-1),solve(a+1),solve(a/x)); // for all x which is prime divisor of a using seive).

    }

    → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    And use memoization

    → Reply
»
6 years ago, # |
← Rev. 3   Vote: I like it +27 Vote: I do not like it

This problem can be solved with Dijkstra. We extend the directed edge from x+1 to x and from x-1 to x. (1 <= x <= 100010) For the prime factor p of x, we extend the directed edge from x/p to x. You can use Dijkstra to find the distance from 1 to A_i. The solution is like this. The time complexity is

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 5   Vote: I like it 0 Vote: I do not like it

    I suppose that the number of edges is NlogN, but in fact, it is 377926 when N = 100010, so it may be considered that the time complexity is .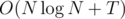

    → Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Yeah, but will not a recursion with memoization work? I think won't , because prime gap is around 100

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +1 Vote: I do not like it

      Before that, did you investigate how your own solution works? I have not seen your code. Since solve (x) calls solve (x + 1) and solve (x + 1) calls solve (x), will not we get out of this infinite loop? If you want to search on this problem, it is bfs from x = 1, not dfs from x = a. I used dijkstra, but if you do a normal bfs you can get an answer in linear time.

      → Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 3   Vote: I like it +5 Vote: I do not like it

    actually, where ω(n) is the number of distinct prime divisors of n and M is the Meissel-Mertens constant. So your solution runs in time.

    → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +4 Vote: I do not like it

    Using BFS instead of dijkstra could improve the solution.

    → Reply
»
6 years ago, # |
  Vote: I like it -9 Vote: I do not like it

build a graph and find the shortest path to reach from node A to node 1 using the Dijkstra algorithm.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +23 Vote: I do not like it

    Your solution will definitely get TLE. The time complexity is O (TNlogN).

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      but his solution is exactly your solution...

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it +8 Vote: I do not like it

        Completely different

        → Reply
        • »
          »
          »
          »
          »
          6 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          How?

          → Reply
          • »
            »
            »
            »
            »
            »
            6 years ago, # ^ |
              Vote: I like it +26 Vote: I do not like it

            Because Reina_Kousaka's solution builds the shortest path tree from node 1, which allows you to answer queries for every node once the Dijkstra is done.

            Meanwhile, constructing a graph from node A only solves the question for that node.

            → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Yes,dijkstra will do it because we have to find all nodes shortest path

    → Reply