On the other hand, I'm happy I didn't spend too much time on it... but yeah, they're too easy. The organisers must be stuck in the last Polish CEOI. If day 2 is also this easy, there are going to be a lot more gold medals.

I know who we can bash for this though: Kamil Dębowski (Scientific Chair).

Lottery was perhaps the easiest task as it requires almost no algorithmic knowledge. Here's the solution:

Lottery

Let B_i, j = δ(a_i ≠ a_j). Now, the distance between some two intervals starting at i and j is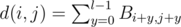 , this can be quickly computed in n² memory using diagonal partial sums on B. The answer to a query k_j is the array c_j where, for each i = 1... n, c_i = g(i, k_j) - 1, where g(i, k_j) is the number of values less than or equal to k_j in the i-th row of the matrix d. We will read all the queries in advance and compute the matrix d row by row. Not surprisingly, the values in the rows are related. From d(i, j) we can compute d(i + 1, j + 1) as follows: d(i + 1, j + 1) = d(i, j) - B_i, j + B_{i + l, j + l}. Here, there's no need to actually store the matrix B, as we can compute its values easily. So, from the previous row of d we can compute all the elements of the current row, except the first element, in O(n). We can compute the first element directly by summing: 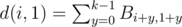, also in O(n). We now "count" the elements of the current row by incrementing u_di for all i, then we compute the partial sum of u, let that be v, and, for each query k_j, add v_kj to the i-th element of c_j. Time complexity: O(n² + nq), memory complexity: O(nq).

Key observation is that we can restrict our moves to taking prefix and moving it down by x. Once spelled out, both proving this and getting entire algorithm from this point is easy.

Here is a rough explanation:

Let's use an observation: Every optimal solution can be described by either decreasing a prefix of the whole array, or increasing a suffix of the whole array.

Informal proof by induction: If we decrease a subarray i...j and we use one at least one element from that subarray, by decreasing element i - 1 as well, we never worsen the LIS. Thus, we can always extend the subarray to 0...j.

An analogous argument also proves that when we increase, we can increase the whole suffix as well without losing solutions.

Another observation lets us combine the two operations of decreasing a prefix and increasing a suffix. If we reverse the array, negate every element t_i and negate x, we can use one function instead of typing two nearly identical functions.

In the solution, for every i s.t. 0 ≤ i < n, we find the LIS of prefix t₀, t₁, ..., t_i that includes t_i, and we find the LIS in t_i + 1, t_i + 2... such that the smallest element in the LIS is larger than t_i - x.

The above can be found in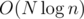 using an extension of this algorithm.

Let's sort all computers and orders by F_i in a global array. Now we can satisfy an order only with computers which are later in the array. So let's go from the right to the left of the array, buy some computers and then sell it for orders.

We can do it maintaining dp_ij, what means maximal profit which we can receive processed the first i objects (computers or orders) from the right and we have exactly j cores. For the full task it's too large memory; so we can easily maintain only one layer dp_j, recalculating it object by object.

Complexity is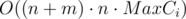 , memory is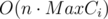

Here is a really short solution.

We combine the list of customers and computers, and sort them according to decreasing clockrate. If there's a tie, we place computers before customers. This ensures that if we have bought any cores, we can use them for any following customer. We use a DP with state UnusedCores with a transition very similar to coin-change DP, and after iterating over every item in reverse order, the answer is dp[0].

Mine is 250 lines, I store differences between indices of consecutive 1s in a balanced BST. There's also no matrix exponentiation, only multiplication.

190 lines, including comments: link. There are some slides describing a solution, but they were meant to help in explaining, not to give the full explanation. I hope they will be uploaded to the website in a day.

A linear solution for each prefix would be:

dp[0] — the number of ways to handle 1's on the right so that they would "touch" the next 1 on the left (so, that next 1 must be changed to some smaller 1's).

dp[1] — the number of ways such that the next 1 on the left can stay in its place.

Quite short implementation of that: link.

Now, we can maintain intervals of type 000001010101, each represented by a matrix 2x2. We can either use BST or we can simulate everything once and gather all the intervals (or indices) that ever appeared, and then build a segment tree over that. I chose the latter approach because I don't like BST's and the tree is much easier this way. The BST solution is also posssible and allowed.

EDIT: and the alternative thing to store is what ksun48 described: distances between consecutive ones.