Пожалуй, я не буду ничего комментировать :D
Автор: GreenGrape
Tutorial is loading...
Автор: GreenGrape
Tutorial is loading...
Автор: GreenGrape
Tutorial is loading...
Автор: GreenGrape
Tutorial is loading...
Автор: ashmelev
Tutorial is loading...
Автор: Errichto
Tutorial is loading...
Автор: Lewin
Tutorial is loading...
Oh well, to be honest I'm so sad that the expected solution for D is indeed O(N3), since 7003 is so strict. I'm coding the same solution but still got TLE instead.
Why is the time limit 1 sec instead of 2 and the bound 700 instead of 500? It's like they want us to TLE...
Maybe we need O(N^3/???) to AC
The Author don't want to let you TLE.He only doesn't want to let the O(n^4) pass. My code with O(n^4) run 919ms on the test which n=500,if n<=500 or time limit is 2 sec I can solve this problem with O(n^4).And my final solution only runs 300ms. P.S. O(n^4)=O(n*n*n*n) P.S.2 There are many (1/2)s in the O(n^4) and O(n^3)'s solution.So n=700 is not so big. Sorry for my poor English.
I had the same problem.I added the heuristic of breaking when an answer is found instead of iterating completely from l to r. this reduced time to 93 ms.
Yes, mine also passed because of the heuristic optimisation. I think that the test cases were weak. I did not even precompute the gcd, still it got AC.
That's a good idea.
I thought O(n3) might be TLE so I used STL bitset. So did fjzzq2002.
I saw that many contestants who coded it iteratively had TL while most of the memoization solutions passed (including mine). This might be caused because a lot of states are practically unreachable.
English tutorial for E?
I don't know how long it will take for an English tutorial, but here is what I did that uses at most 4n2 moves:
1) Get every block into their own row. What I did to accomplish this is to push every block in the first column up as high as they can. So, if there are k0 blocks in the first column, they take rows 1... k0. Then, I take the blocks in the second column--let's say there are k1 of them--and push them into position k0 + 1... k0 + k1. Do this for each column.
2) Now that each block is in its own row, I want to get them each to their own column, but in a specific way. Let's say that, in the end, a0 blocks need to end up in the first column. Then, I make sure that those a0 blocks take up the first a0 columns (1... a0). Then, similarly, if a1 blocks need to be in the second column by the end, then I make sure to move those blocks into columns a0 + 1...a0 + a1. Do this for every column.
3) Now that each block is in their own column, simply move each one to its final row.
4) Now you should be able to move each block into its final column. Even though there can be multiple blocks in a row, they will appear in the same order that they have to be in the end due to our work in step 2. Thus, each block can be shifted within its own row to its correct spot.
Everything here can be accomplished pretty nicely with code. My submission: 41868501
Could you elaborate at step 1? I mean is there any nice way to implement shifting x cubes in given colum to positions i...i+x-1?
There exists O(N3 / WordSize) solution for D:
At first we need calculate bitset good[i] for each i, where good[i][j] is gcd(a[i], a[j]) > 1.
We need 3 dps:
Now we could calculate each can[left][right] = canLeft[left] && canRight[right].
After that we need update canLeft[left][right + 1] = can[left][right] && good[right + 1]
(canRight[right][left - 1] can be updated in the same way).
Each operation is O(N / WordSize), so total complexity is O(N2·N / WordSize) = O(N3 / WordSize).
Link to AC solution with this algorithm: https://codeforces.net/contest/1025/submission/41855097
Can you explain what is the word size?I can't understand it.
64, it is length of
long long intThank you very much
Well, the worse you can do in a competition is getting rejected just because some a*****e copied your solution from ideone.com. Not gonna use ideone.com anymore for contests.
The message I received:
Attention! Your solution 41833175 for the problem 1025A significantly coincides with solutions cfbfgf/41832971, rahul1995/41833175, getSchwifty/41833466. Such a coincidence is a clear rules violation. Note that unintentional leakage is also a violation. For example, do not use ideone.com with the default settings (public access to your code). If you have conclusive evidence that a coincidence has occurred due to the use of a common source published before the competition, write a comment to post about the round with all the details. More information can be found at http://codeforces.net/blog/entry/8790. Such violation of the rules may be the reason for blocking your account or other penalties.
You can still use IdeOne, but make your code secret.
I always wondered why people use ideone instead of a compiler/IDE on a local machine.
The program on my computer takes longer
You can also use repl.it
Some people have used some online resources and have got plagiarism message,check the third party rule is changing blog
Anyone knows anything faster than N^3 for D? For someone who sucks at implementation, I don't think I would dare submit such a solution when N = 700 (especially when task doesn't even give use 2 seconds)
Even idea toward a faster solution would be appreciated, thanks!
There is idea of solution in O(N3 / WordSize) with bitsets:
https://codeforces.net/blog/entry/61323?#comment-452741
My solution with Divide and Conquer with memoization has asymptotic complexity O(n3) as 1021839 pointed out, however the actual maximum number of operations is n * 1 + (n - 1) * 2 + (n - 2) * 3 + ... + n (the length of every [l, r] segment multiplied by the amount of such segments) which for n = 700 results in < 108 operations, which fits inside 1 second ... the idea is to try to make each element the root, and split the array into two subarrays and recursively solve for them. The parent of a subarray can either be r+1 or l-1, and those are the memoized states.
Code: 41859995
Note that this is only a recursive implementation of the editorial, but explains why it works for n=700 without much problems.
Your
dacfunction is in fact O(N3), since there are up to N2 possible states and each state takes O(r - l) time to process. (There might be a stronger bound on this DP than O(N3) overall, but if so I'm not aware of it.)Usually an author is given just after an editorial for a corresponding problem. So don't get confused: I invented F, not E :D
also, my code if someone wants to take a look: link.
The code is pretty clean, but I don't understand exactly what are you doing? Sorting vectors that each pair creates by what, how does that make L and R the k1 and k2 from the editorial?
Could you elaborate on the loop that looks like two pointers a bit more?
Thanks,
L and R in my code denote the number of points on left and right from the line (k1 and k2 from the editorial).
And yes, I use two pointers. I iterate over point p in one half, and move index iL of some point in the other half.
Thank you for clarifying that part.
However, I still do not understand how did you exactly sort the vectors, what does your operator < function for comparison of two points (in this case vectors from one point to another it would appear) mean?
nice tutorial for c. Thank You!
Can someone please explain the intuition behind using DP for Problem D?
If you take some binary search tree (BST) and write it's values in increasing order — every subtree will be presented as subarray of result array.
Now we have that result array and we need find if there exists possibility to build some BST with edge constraint from statement.
As we know, each subtree in BST consists of root, left subtree and right subtree. In array it will be presented as index root and two subarrays [left... root - 1] and [root + 1... right].
So we could use dynamic programming dp[left][right][root] — "could we build BST on subarray [left... right] and root is root (left ≤ root ≤ right)".
Let's use additional matrix canEdge[i][j] — "can we build edge between a[i] and a[j]: gcd(a[i], a[j]) > 1".
Now we could write formulas for calculating dp:
At this moment our dp already can be calculated in O(N3) with formulas above, but it has O(N3) states that is not so good for memory.
Let's store only trees where root is the left one or the right one — dp[left][right][isRootRight] (0 is for the left, 1 — for the right) :
Now answer for whole array is true if exists some root that dp[left][root][1] && dp[root][right][0].
New dp has only O(N2) states but calculates in O(N3) as previous one.
Wow, Thanks for such a wonderful answer!!
For your 2nd point shouldn't it be :
dp[left][right][left < root < right] = dp[left][root-1][root] && dp[root+1][right][root]?Sorry correct me if I am wrong!
No, it's correct.
By definition of dp root should be inside subarray, but [left... root - 1] and [root + 1... right] don't contain root inside.
This formula means "if you have some correct tree where root is the right one and other tree where the same root is the left one — you can merge them in one tree".
Okay!! Thanks a lot for reply and for wonderful answer. Indeed it helped a lot.
I understand the solution but only after seeing the editorial. During the contest I got the fact that it's a DP problem and very similar to matrix chain multiplication but I was not able to reduce it to O(N^3). It would be helpful if you provide some insights on how you think about optimizations in DP ? That's a less touched topic I believe.
You're right, this is a topic that is rarely touched on at all. In fact, the optimizations are usually just given right away in the editorial without much motivation (not knocking the author; it's difficult to write out the motivation well if you already know the solution). I'll try to explain my thought process on the DP optimization problems I've done. Keep in mind I'm not too high rated, so I've only done a handful of DP problems where optimization was needed for AC, so I won't be talking about anything like convex hull trick or Knuth optimization.
My original O(n^4) DP was dp[l][r][k], where dp[l][r][k] = 1 if you can create a subtree on [l, r] with k as the root (l ≤ k ≤ r), and 0 otherwise. This had linear updates, and I imagine this was what most people's first iteration of the DP was.
In general, the reason one can do DP optimizations is if many states being stored are actually unnecessary, or can be encapsulated in another state. Storing [l, r] seems necessary, since the subarrays can differ and the BSTs will vary wildly, so that's probably not where we look to optimize. However, let's look at k, the root of the subtree. Why exactly are we storing the root? Well, you might argue, it's because when we are recursing on node i as the root, we need to know if one of the possible roots of [i+1, r] is not coprime to node i.
But wait, that's the thing. We only need to know if ONE of the possible roots is not coprime. We don't actually need to store every root that works. And for the subtree on [l, r], the only possible parents of this subtree are l-1 and r+1. So all we need to check in [l, r] is if any of the possible roots are not coprime to l-1 and r+1. That should reduce the state to O(n^2), with linear updates, so O(n^3) (Note: PRECALCULATE GCDs OF PAIRS).
I hope that was somewhat insightful, since that was my (very abridged) thought process during the contest.
Can you explain me the intuition behind the isRight state in your DP?
if someone interested , here is the implementation of Slamur's idea. https://codeforces.net/problemset/submission/1025/44717178
Thanks Bro for your great effort.
Fundamentally, one should use DP if a problem can be solved by solving subproblems of an identical structure, and these subproblems get repeated when trying to find a solution.
The biggest key to noticing that you need DP is that BSTs are recursively defined data structures, i.e. the left subtree and right subtree of any node are both BST's themselves. Say you are trying to solve the problem on all the nodes from [0, n-1]. You know that some node i will be the root. Then, you notice that you need to solve the exact same problem as the original one, but on the nodes [0, i-1] and [i+1, n-1]. That should be the observation that immediately triggers "DP" to pop into your head.
There is a different, very nice solution for problem B, working in O(Nlog4e18) time. Click here to find my implementation from the contest. This solution requires more reasoning, but is significantly easier to implement.
Firstly, let’s define a|b as meaning that a is a factor of b, so there exists some integer k such that b = a * k. Let’s firstly consider any prime p. Consider any input pair (a, b). If p is to be a solution of the problem, then p|a or p|b for every input pair (a, b). However, since p is prime, this is equivalent to saying that p|a * b for every input pair (a, b).
Let’s consider the value curr, which is initially set to 0. For every pair (a, b) in the input, let us set curr = gcd(curr, a * b). (Here we assume that gcd(0, x) is equal to x.) In other words, we have that curr = gcd(a0 * b0, a1 * b1, …, aN * bN). Let us consider any prime factor p that may have been a solution to the problem. If it may have been a solution to the problem, that means that p|a * b for every input pair (a, b), as we have shown above. Therefore, if p divides every product a * b, p must also divide the gcd of every product a * b, which means that p|curr. Therefore any prime number which may be a solution is a factor of curr. Now, let us consider any prime factor p of curr. Obviously since p|curr, then p|a * b for every input pair (a, b), so p|a or p|b. Therefore, any prime factor of curr is a solution to the problem. As a result, this means that curr has prime factors which correspond exactly to the prime solutions to the problem.
Now, let’s consider the case that curr = 1. When this is the case, since we have shown above that curr has prime factors which correspond exactly to the prime solutions to the problem, since 1 has no prime factors, there are no prime numbers which are solutions to the problem. Now, let us consider any possible solution to the problem, if one exists. If s is some solution, then it is obviously the case that any prime factor p of s is also a solution. However, since no prime numbers p are solutions, then if s has any prime factors it is also not a solution. Therefore the only solution in this case is s = 1, which by the problem constraints is not a solution at all. Thus, in this case, we must output - 1.
Let us now consider the other case, where curr > 1. We will show that, if we consider every pair (a, b) one more time, and do curr = gcd(curr, a) if gcd(curr, a) > 1 else curr = gcd(curr, b), then we can output curr, and it will always be a solution. Firstly, let’s prove that doing this method will always produce a solution to the problem or 1. If we consider this method, then by definition, since we take the gcd of curr with either a or b from every pair, that means that curr|a or curr|b after every pair we process. Therefore, our final result curr will divide a or b for every single pair (a, b). The only problem here is that curr might be equal to 1. We will now prove that, if you use the method above, this will not happen. Let us assume that curr is initially greater than 1, before processing some pair (a, b). This means that curr has at least one prime factor p; let’s consider any prime factor p. We know from our definition of curr that p|a * b for every pair (a, b), which means that p|a or p|b. Let us assume, without loss of generality, that p|a. (If p|b instead, then we can reverse our reasoning and arrive at the same result.) Since p|a, that means that there is some integer x such that a = x * p. In addition, there is some integer y such that curr = y * p, since p|curr. Therefore, gcd(curr, a) = gcd(y * p, x * p) = p * gcd(x, y) ≥ p. As a result, any prime factor p of curr that was initially a factor of a will be preserved, and curr will always be greater than 1 after processing each step, assuming that it was originally greater than 1 (which it was). Therefore, using this method, our final result for curr will always be such that curr|a or curr|b for every input pair (a, b), and also curr > 1. Thus, in this case, not only is there always a solution, but we can generate it using this above method in O(Nlog4e18) (the log4e18 comes from gcd finding).
very cool reasoning. I have a question derived from this one. If change the definition of WCD to :select arbitrary one number from each pair,let the GCD of all these n numbers be WCD, is there an efficient way to find a solution?
I don't quite understand what your question is. If you consider the GCD of all n numbers for every possible selection within each pair, then every single GCD that you find will be a valid WCD, and every factor of these will be as well. So your change of definition is only a very minor one. As a matter of fact, the solution I propose above will always find some number that is a WCD according to your definition (if one exists).
thanks for reply to me.I think you misunderstood my definition as WCD = gcd(gcd(set1),(set2),......(setn)), where setimeans one possible selection. but mine is just like WCD = gcd(seti), seti means an arbitrary selection of all possible selections. thus, for some input, there may be multi different WCDs, if WCD can only be 1,print -1, else print any possible WCD greater than 1. If input is:
in my definition, answer could be gcd(6, 30) = 6 or gcd(15, 30) = 15, but in the original problem, answers include 2, 3 and 5. That's the difference. So, is there an efficient way to find a such WCD greater than 1 if there exists any?
I see. I'm pretty convinced that the solution I give above actually works for this problem as well. The value of curr will always correspond to the GCD of seti for some selection seti. In addition, it will also correctly determine whether or not such a WCD greater than 1 exists. It may be a useful exercise to attempt proving this for yourself (or disprove it).
I will rethink it , Thanks a lot.
Cool solution. I'd like to share my (a little different) way to deal with this problem B ( code ). The idea is to take GCD of all pair's LCM, let it be 'allGcd'. Then any prime factor allGcd will be the answer, because it's a factor of at least one number in a pair. But allGcd may be up to 1e18, so we can just take GCD of it and one of the numbers in one of the pairs (the one, which doesn't return 1, if such exists), reducing allGcd at least to 1e9. Finally, we iterate up to sqrt(allGcd) to find first number, which is a factor (it will be prime, so we got what we wanted)
Nice idea. Out of interest, and to check whether or not I actually understand your solution, is it necessary to take the lcm? Because it seems to me that you could just take the gcd of the products a * b, and then try the gcds with a[0] and b[0] respectively as you do.
Actually you're right, didn't think about it earlier
As this points out, if you were to have:
such that x and y are primes > 109 , their lcm() will be their product which is > 1e18.So you can't loop to it's sqrt().
Instead, you can find the prime factors of a[0] and b[0] and return any one of them that divides allGcd.
That's why I reduce it at least to 1e9 by taking GCD of allGcd with a[0] and allGcd with b[0], when choose the one, which isn't 1
Oh yes you're right I didn't read that
Why at the end we have to again take gcd with any one pair?? "so we can just take GCD of it and one of the numbers in one of the pairs"
Because sqrt(allGcd) may be up to 1e9, so it will be TLE. By taking GCD with one pair we guarantee that allGcd will become < 2e9, so cycle to sqrt won't be too long
for problem B, can i say the max (number of divisor) from number 2 <= x <= 2*(10^9) is largest number of 2*3*4*5....(n times) that not exceed 2*(10^9) ? if so, i try to calculate it and it has only max 11 divisor, so at first a[0] and b[0] can have 22 divisor (my approach is generate initial divisors that can be the answer, that is number that divide first number or second number at the most top input).
my implementation using set to store the initial divisor, for each pair 1 to n, traverse the set, if the number cant divide first pair and cant divide second pair, delete it from the set. so at worst no deletion (because each times traverse 22 number on set?) and the worst case is sqrt(2*(10^9)) + 150k*22 < 10^8 (expected 1s) operation, but my code TLE, why?
2*3 is 6 so you would multiply that twice. Number with most divisors below 10^9 has more than 1000 divisors
What about the editorials for Round #504 ??
Can anyone give more details of a rigorous analysis of G?
Are you familiar with how to use martingales to analyze random walks? If so, this technique is very similar.
I skipped some steps in defining what exactly my random variable is. Here it is specifically. Let Xi be a random variable representing the expected value of the potential at time i minus i.
From the analysis, it is not too hard to show that E(Xi + 1|X0, X1, ..., Xi) = Xi (this is because our expected potential increases by one, and also i increases by one, so there is no change in the expected value).
We have some unknown stopping time T, we know that XT = 2n - 1 - 1 - T, and the problem is to find E(T), which is equal to E(2n - 1 - 1 - XT).
Using the optional stopping theorem, we have E(XT) = E(X0). So, we have E(T) = 2n - 1 - 1 - E(X0). We already know how to compute E(X0), which is just the current potential of the state.
Hi, lewin. Can I ask a question on how to define the potential? It's still not very clear to me. My guess of the procedure is:
Let the potential to be f(k), p and q to be the numbers of followers for two selected startups. Then the difference of the potentials after a step is: [p * f(0) + f(q + 1) + q * f(0) + f(p + 1)] / 2 - f(p) - f(q)
And we want to the difference to be constant, so we can choose f(k) = 2k - 1. Is this similar to what you think?
for problem(B) how can we find the prime factorization of number upto 10^9 in logn time ..if we make the seive of lowest prime divisors..even that can be made just upto 10^6 which will find prime divisors for numbers <=10^6 ..please somebody explain how to do it
Finding the prime factorization is done is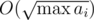
time. But since there are only 
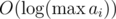primes, doing the linear divisibility check for each prime takes a total of 
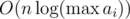time.
sorry, but i didn't understand how there are only distinct mehrunesartem(10^9) primes to be checked out and what they are, please explain it a bit more
The number of distinct prime factors of a number k is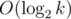
. It's a good exercise to think about why.
Hint: Think about approximately how many non distinct prime factors there are in k (in terms of big-O). Is this more or less than the number of distinct prime factors?
If you're having trouble figuring out how many non distinct prime factors there are in k, here's another hint: What if the only prime factor was 2? How many non distinct prime factors are there? Again, is this more or less than the total number of non distinct prime factors?
i know that the number of distinct prime divisors can be at max O(logn) for 'n', initially i mistakenly thought about creating 'n' union set of distinct prime divisors and then iterating through them to find a number which is present in all sets which is even possible if a,b <=10^6. now after seeing your code things are clear that we are just doing all work for a random pair to get its union set of prime divisors, and then just checking for each element in set because if answer exist then it must be present in this set..overall thanks a lot, learnt few things.