i have solved two similar problem recently 1027F & 875F
To solve 1027F i tried approach this problem using binary search and dsu but i am getting tle but my straightforward solution using kuhn`s algorithm got AC.
Can anyone explain the reason behind it? why kuhn`s is so fast here and why my dsu with binary search got TLE.
links to my submission
and to makes things more complicated for me
875F i tried this problem using kuhn got tle but i got AC using DSU.
links to my submission
it will be very helpful if anyone can explain this to me!! when and where should i use DSU or kuhn!!
kind regards
I think that the reason is in the tests.
That will be very odd.
Also in 1027F (DSU solution) you can do binary search only on values from input (decreasing complexity from log(109) to log(2 * 106)).
Thanks I will do that
I successfully submitted your code with DSU in
3s. This is what I changed:In your solution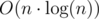
recursive calls in DSU, so now this is implemented without recursion
Now your code does not contain static arrays, only modern C++ vectors
Added
pragma GCC optimize ("O3")Fastest input in C++ with
freadI don't know which modifications more helpful, but all its in union lead to accepted solution. U can try to apply one or more of them. But with optimizations O3 you can't guaranteed accepted solution in more than one identical submission in various time, because some optimizations in this groups depends on magic.
Your solution works in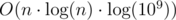
, but log(n) it is not log2(2·106) ≈ 21, it is 
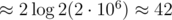+ bigger hidden constant from random access to large vectors in dynamic memory. In case when you have small vectors all values in caches of processor, so it's fast to access, but in case when you have 2 - 3 vectors on 2·106 elements it is very slow to random access to memory (get parent of parent of vertex, for example).
thank you it was very helpful for me!