AIM Tech Round 5 Editorial

№	Пользователь	Рейтинг
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

№	Пользователь	Вклад
1	cry	167
2	Um_nik	163
3	maomao90	162
3	atcoder_official	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	Dominater069	153
9	nor	153

Thanks bmerry for posting his solutions, we gently took some of them as a base for editorial.

Tutorial is loading...

Problem author: VadymKa

Problem developers: riadwaw, malcolm

Code

static class SquareInside {
        final int inf = (int) 1e9;

        public void solve(int testNumber, InputReader in, PrintWriter out) {
            int n = in.readInt(), m = in.readInt();
            char[][] s = new char[n][];
            for (int i = 0; i < n; i++) {
                s[i] = in.readWord().toCharArray();
            }
            int minX = inf, maxX = -inf, minY = inf, maxY = -inf;
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < m; j++) {
                    if (s[i][j] == 'B') {
                        minX = Math.min(minX, i);
                        minY = Math.min(minY, j);
                        maxX = Math.max(maxX, i);
                        maxY = Math.max(maxY, j);
                    }
                }
            }
            out.print((minX + maxX) / 2 + 1);
            out.print(' ');
            out.println((minY + maxY) / 2 + 1);
        }

    }

Tutorial is loading...

Problem author: VadymKa

Problem developers: riadwaw, malcolm, Kostroma, Errichto

Code

  int len = 400;
  cout << string(len, '5') << "\n";
  cout << (string(len - 1, '4') + '5') << "\n";

Tutorial is loading...

Problem author: malcolm

Problem developers: yarrr, Edvard, malcolm, Errichto

Code

static class Rectangle {
        public Point topLeft, bottomRight;

        public Rectangle(Point topLeft, Point bottomRight) {
            this.topLeft = topLeft;
            this.bottomRight = bottomRight;
        }

        public Rectangle intersect(Rectangle other) {
            if (other == null) {
                return null;
            }
            int x0 = Math.max(topLeft.x, other.topLeft.x);
            int y0 = Math.max(topLeft.y, other.topLeft.y);
            int x1 = Math.min(bottomRight.x, other.bottomRight.x);
            int y1 = Math.min(bottomRight.y, other.bottomRight.y);
            if (x0 > x1 || y0 > y1) {
                return null;
            }
            return new Rectangle(new Point(x0, y0), new Point(x1, y1));
        }
    }

    private void solve() throws IOException {
        int rectanglesCount = nextInt();
        Rectangle[] rectangles = new Rectangle[rectanglesCount];
        for (int i = 0; i < rectanglesCount; i++) {
            Point topLeft = new Point(nextInt(), nextInt());
            Point bottomRight = new Point(nextInt(), nextInt());
            rectangles[i] = new Rectangle(topLeft, bottomRight);
        }
        Rectangle[] prefixIntersection = new Rectangle[rectanglesCount + 1];
        Rectangle[] suffixIntersection = new Rectangle[rectanglesCount + 1];
        prefixIntersection[0] = suffixIntersection[0] = new Rectangle(
            new Point(Integer.MIN_VALUE, Integer.MIN_VALUE),
            new Point(Integer.MAX_VALUE, Integer.MAX_VALUE)
        );
        for (int i = 1; i <= rectanglesCount; i++) {
            prefixIntersection[i] = rectangles[i - 1].intersect(prefixIntersection[i - 1]);
            suffixIntersection[i] = rectangles[rectanglesCount - i].intersect(suffixIntersection[i - 1]);
        }

        for (int i = 0; i <= rectanglesCount; i++) {
            if (prefixIntersection[i] != null) {
                Rectangle intersection = prefixIntersection[i].intersect(suffixIntersection[rectanglesCount - i - 1]);
                if (intersection != null) {
                    out.println(intersection.topLeft);
                    return;
                }
            }
        }
        throw new AssertionError();
    }

Bonus: Solve the problem, if you need to find intersection of some n - k of n rectangles, if k ≤ 10. Without data structures.

Tutorial is loading...

Problem author: Errichto

Problem developers: zemen, Errichto, Kostroma, riadwaw

Code

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using ld = long double;

const int mod = 1e9 + 7;

signed main() {
#ifdef LOCAL
  assert(freopen("test.in", "r", stdin));
#endif
  int n;
  cin >> n;
  map<int, int> a{{INT_MIN, 1}, {INT_MAX, 0}};
  set<int*> non0{&a.begin()->second};
  for (int i = 0; i < n; ++i) {
    string t;
    int x;
    cin >> t >> x;
    if (t == "ADD") {
      auto it = a.lower_bound(x);
      assert(it != a.begin());
      --it;
      int ways = it->second;
      auto m = a.emplace(x, ways).first;
      non0.insert(&m->second);
    } else {
      auto m = a.find(x);
      assert(m != a.end() && m != a.begin());
      auto it = prev(m);
      auto& w = it->second;
      w = (w + m->second) % mod;
      non0.insert(&it->second);
      non0.erase(&m->second);
      a.erase(m);
      for (auto it2 = non0.begin(); it2 != non0.end(); ) {
        if (*it2 == &it->second) {
          ++it2;
        } else {
          *(*it2) = 0;
          it2 = non0.erase(it2);
        }
      }
    }
  }
  int res = 0;
  for (auto p : a) {
    res = (res + p.second) % mod;
  }
  cout << res << '\n';
}

Tutorial is loading...

Problem author: zemen

Problem developers: yarrr, Kostroma

Code

void solve(__attribute__((unused)) bool read) {
  int n;
  cin >> n;
  vector<int> b(n, 0);
  for (int i = 0; i < n; ++i) {
    cin >> b[i];
  }
  int mx = *max_element(all(b));
  int start_pos = -1;
  for (int i = 0; i < n; ++i) {
    if (b[i] == mx && b[(i - 1 + n) % n] != mx) {
      start_pos = i;
      break;
    }
  }
  if (start_pos == -1) {
    if (mx == 0) {
      cout << "YES\n";
      for (int i = 0; i < n; ++i) {
        cout << 1 << " \n"[i + 1 == n];
      }
      return;
    }
    cout << "NO\n";
    return;
  }
  auto a = b;
  for (int i = 1; i < n; ++i) {
    int pos = (start_pos - i + n) % n, prev_pos = (start_pos + 1 - i + n) % n;
    a[pos] += a[prev_pos];
    if (i == 1) {
      a[pos] += mx;
    }
  }
  cout << "YES\n";
  for (int x : a) {
    cout << x << " ";
  }
  cout << "\n";

}

Tutorial is loading...

Problem author: Errichto

Problem developers: Kostroma, malcolm

Code

struct Point {
  int x, y;
  Point() {}
  Point(int x, int y) : x(x), y(y) {}
  void scan() {
    cin >> x >> y;
  }
  auto key() const {
    return make_pair(x, y);
  }
  bool operator < (const Point& ot) const {
    return key() < ot.key();
  }
  bool operator == (const Point& ot) const {
    return key() == ot.key();
  }
  Point operator + (const Point& ot) const {
    return Point(x + ot.x, y + ot.y);
  }
  li sqr_dist() {
    return x * 1LL * x + y * 1LL * y;
  }
  void normalize() {
    auto g = gcd(x, y);
    x /= g;
    y /= g;
  }
};

struct Hasher {
  size_t operator () (const Point& pt) const {
    return pt.x * 2352345 + pt.y;
  }
};

enum Type {
  INSERT = 1,
  REMOVE = 2,
  QUERY = 3
};

struct Query {
  Type type;
  Point pt;
  int dist_id;
  void scan() {
    int type1;
    cin >> type1;
    type = Type(type1);
    pt.scan();
  }
};

void solve(__attribute__((unused)) bool read) {
  int Q;
  cin >> Q;
  vector<Query> queries(Q);
  map<li, vector<Point>> all_points;
  vector<li> dists;
  set<Point> have;
  for (int i = 0; i < Q; ++i) {
    queries[i].scan();
    auto& pt = queries[i].pt;
    if (queries[i].type != QUERY) {
      all_points[pt.sqr_dist()].push_back(pt);
      dists.push_back(pt.sqr_dist());
    } else {
      pt.normalize();
    }
  }
  make_unique(dists);
  for (auto& q : queries) {
    q.dist_id = (int)(lower_bound(all(dists), q.pt.sqr_dist()) - dists.begin());
  }
  vector<vector<char>> has_point(dists.size());
  vector<vector<Point>> points_by_dist_id(dists.size());
  vector<vector<vector<Point>>> sum_points(dists.size());
  unordered_map<Point, pair<int, int>, Hasher> point_position;
  for (auto& item : all_points) {
    make_unique(item.second);
    int dist_id = (int)(lower_bound(all(dists), item.first) - dists.begin());
    has_point[dist_id].assign(item.second.size(), false);
    points_by_dist_id[dist_id] = item.second;
    sum_points[dist_id].assign(item.second.size(), vector<Point>(item.second.size()));
    for (int i = 0; i < item.second.size(); ++i) {
      point_position[item.second[i]] = {dist_id, i};
      for (int j = 0; j < item.second.size(); ++j) {
        sum_points[dist_id][i][j] = item.second[i] + item.second[j];
        sum_points[dist_id][i][j].normalize();
      }
    }
  }
  unordered_map<Point, int, Hasher> on_line;
  unordered_map<Point, int, Hasher> good_pairs;

  auto change_on_line = [&] (Point pt, bool add) {
    pt.normalize();
    if (add) {
      ++on_line[pt];
    } else {
      assert(on_line[pt] > 0);
      --on_line[pt];
    }
  };

  int n_points = 0;
  for (auto& cur_q : queries) {
    auto& pt = cur_q.pt;
    int dist_id = cur_q.dist_id;
    if (cur_q.type == INSERT) {
      ++n_points;
      int pos = point_position[pt].second;
      assert(!has_point[dist_id][pos]);
      change_on_line(pt, true);
      for (int i = 0; i < points_by_dist_id[dist_id].size(); ++i) {
        if (i == pos || !has_point[dist_id][i]) {
          continue;
        }
        ++good_pairs[sum_points[dist_id][i][pos]];
      }
      has_point[dist_id][pos] = true;
    } else if (cur_q.type == REMOVE) {
      --n_points;
      int pos = point_position[pt].second;
      assert(has_point[dist_id][pos]);
      change_on_line(pt, false);
      for (int i = 0; i < points_by_dist_id[dist_id].size(); ++i) {
        if (i == pos || !has_point[dist_id][i]) {
          continue;
        }
        --good_pairs[sum_points[dist_id][i][pos]];
      }
      has_point[dist_id][pos] = false;
    } else if (cur_q.type == QUERY) {
      pt.normalize();
      cout << n_points - 2 * good_pairs[pt] - on_line[pt] << "\n";
    }
  }

}

Tutorial is loading...

Problem author: zeliboba

Problem developers: Kostroma, riadwaw

Code

private static final int MAX_WIDTH = 10000;
    private static final int QUERIES = 5;
    public static final long INF = 20000000000000000L;
    long[][] memo = new long[QUERIES + 1][MAX_WIDTH + 1];

    long dp(int guesses, long l) {
        if (guesses == 0) {
            return l;
        }
        if (l > MAX_WIDTH) {
            return Math.min(INF, dp(guesses, MAX_WIDTH) + l - MAX_WIDTH);
        }

        if (memo[guesses][(int) l] != 0) {
            return memo[guesses][(int) l];
        }
        long ans = l;
        for (int i = 0; i < l; ++i) {
            ans = dp(guesses - 1, ans);
            ++ans;
        }
        ans = dp(guesses - 1, ans);
        return memo[guesses][(int) l] = Math.min(ans, INF);
    }
    private void run() throws IOException {
        long l = 1;
        long r = dp(QUERIES, 1);
        for (int queriesNext = QUERIES - 1; queriesNext >= 0; --queriesNext) {
            List<Long> query = new ArrayList<>();
            long curL = l;
            for (int i = 0, e = (int)Math.min(l, MAX_WIDTH); i < e; ++i) {
                long end = dp(queriesNext, curL);
                query.add(end);
                curL = end + 1;
            }
            assert r == dp(queriesNext, curL);
            out.print(query.size());
            for (long x: query) {
                out.print(" ");
                out.print(x);
            }
            out.println();
            out.flush();
            System.out.flush();

            int ans = readInt();
            if (ans < 0) {
                return;
            }
            if (ans > 0) {
                l = query.get(ans - 1) + 1;
            }
            if (ans != query.size()) {
                r = query.get(ans);
            }

            assert dp(queriesNext, l) == r;
        }
    }

Tutorial is loading...

Problem author: Kostroma

Problem developers: Kostroma, riadwaw, gchebanov, malcolm

Code

const int C = 5032107 + 1;
int lp[C];
int fred[C];
int num_primes[C];

const int MAX_DIVISORS = 7;
const int MAX_ANS = 2 * MAX_DIVISORS;

int max_left[MAX_DIVISORS + 1][C];
int max_border[MAX_ANS + 1];

vector<int> cur_primes;

vector<int> divs;

void get_divisors(int n) {
    divs = {1};
    while (n > 1) {
        int p = lp[n];
        n /= p;
        int sz = divs.size();
        for (int i = 0; i < sz; ++i) {
            divs.push_back(divs[i] * p);
        }
    }
}

void solve(bool read) {
    vector<int> pr;
    for (int i = 2; i < C; ++i) {
        if (lp[i] == 0) {
            lp[i] = i;
            pr.push_back(i);
        }
        for (int j = 0; j < pr.size() && pr[j] <= lp[i] && i * pr[j] < C; ++j) {
            lp[i * pr[j]] = pr[j];
        }
    }
    fred[1] = 1;
    for (int i = 2; i < C; ++i) {
        int p = lp[i];
        int cur = i / p;
        if (cur % p == 0) {
            fred[i] = fred[cur / p];
            num_primes[i] = num_primes[cur / p];
        } else {
            fred[i] = p * fred[cur];
            num_primes[i] = num_primes[cur] + 1;
        }
    }

    for (int i = 0; i < C; ++i) {
        for (int j = 0; j <= MAX_DIVISORS; ++j) {
            max_left[j][i] = -1;
        }
    }
    memset(max_border, -1, sizeof(max_border));

    int n;
    cin >> n;
    int Q;
    cin >> Q;
    vector<int> a(n);
    for (int i = 0; i < n; ++i) {
        cin >> a[i];
        a[i] = fred[a[i]];
    }

    vector<vector<pair<int, int>>> queries(n);

    vector<int> res(Q);
    for (int i = 0; i < Q; ++i) {
        int l, r;
        cin >> l >> r;
        --l; --r;
        queries[r].push_back({l, i});
    }

    for (int i = 0; i < n; ++i) {
        get_divisors(a[i]);
        for (int d : divs) {
            int first_add = num_primes[a[i]] - num_primes[d];
            for (int prev_ans = 0; prev_ans <= MAX_DIVISORS; ++prev_ans) {
                int cur_left = max_left[prev_ans][d];
                int cur_ans = first_add + prev_ans;
                if (cur_ans <= MAX_ANS) {
                    relax_max(max_border[cur_ans], cur_left);
                }
            }
        }
        for (int d : divs) {
            int first_add = num_primes[a[i]] - num_primes[d];
            relax_max(max_left[first_add][d], i);
        }
        for (auto q : queries[i]) {
            res[q.second] = MAX_ANS + 1;
            for (int cur_ans = 0; cur_ans <= MAX_ANS; ++cur_ans) {
                if (max_border[cur_ans] >= q.first) {
                    res[q.second] = cur_ans;
                    break;
                }
            }
            assert(res[q.second] <= MAX_ANS);
        }
    }

    int sum_ans = 0;
    for (int i = 0; i < Q; ++i) {
        cout << res[i] << '\n';
    }
}

Комментарии (64)

Показать архивные | Написать комментарий?

allllekssssa

6 лет назад, # |

+40

It is really funny that I used totally same constructive algorithm in B task, same amount of 9 and all other digits :)

→ Ответить

Harshad

How to solve C if we are asked to find any point which lies in maximum number of Rectangles?

SerezhaE

6 лет назад, # ^ |

+27

Let's compress all values and sort points by x-coordinate. Now we can see that there is two types of events: some rectangle "opens" and some rectangle "closes". So we can solve this problem with scanline on x-axis using any data structure that can add 1 on [l, r], subtract 1 on [l, r] and tell a position of maximum value in all structure (i.e. segment tree is good for this task).

vivace_jr

SerezhaE how will you find the corresponding y-coordinates?

+21

We have a segment tree built on y-axis, therefore for each y we know how many rectangles cover point (x_current, y). I think it is not hard to determine an y in which maximum value is reached – just start at the root of segment tree and further at every step go to the son with bigger maximum value.

ShakuganSky

-18

I think scanline technique on x coordinate while maintaining a segment tree on y coordinate would be helpful in that case. Actually, I coded that solution during the contest, which wasted me like 30 minutes or so. XD

izanbf

← Rev. 2 →

-13

Find the intersecting segments in X and Y axis, then merge both results to get intersecting rectangle. It can be solved easily in O(n log n) using multisets: 42187139

Why so many downvotes?

kmyiu

Some Intuition on solving Problem E:

Notice that b₁ = a₁ mod a₂, so we can write a₁ = b₁ + x₁a₂ for some non-negative integer x₁.

Similarly a₂ = b₂ + x_2a₃. By substituting back continuously we have a₁ = b₁ + x₁b₂ + ... + x₁x₂...x_n - 1b_n + x₁x₂...x_na₁.

Hence x₁x₂...x_n = 0 or b₁ = b₂ = ... = b_n = 0. Also x_i can be zero (i.e. a_i = b_i) only if b_i - 1 < b_i. by the definition of modulo operation. Fix some a_j = b_j satisfying the above condition, then generate appropriate a_j - 1 and so on such that a_k > b_k - 1 for every k.

mohamedeltair

Very nice, thank you.

changxv

I don't know how to generate a_j - 1.

t=b[i-j-1]-b[i-j];
t++;
if(t>0){
  m=t/a[i-j+1];
  if(t%a[i-j+1]) m++;
  a[i-j]=b[i-j]+a[i-j+1]*m;
}

Could you tell me what do these mean？

The condition for appropriate a_k - 1 is a_k - 1 > b_k - 2 , i.e. b_k - 1 + x_k - 1a_k > b_k - 2 or x_k - 1a_k ≥ b_k - 2 - b_k - 1 + 1. If RHS > 0 then x_k - 1 ≥ ceil((b_k - 2 - b_k - 1 + 1) / a_k).

Thank you very much!!!：）

Ghost0fSparta

← Rev. 3 →

Can anybody tell me what is wrong with my solution for problem C. I have used same concept as in editorial but am getting WA on testcase 14. Solution
UPD: NEVERMIND FOUND A TYPING MISTAKE

amityadav

you'r algo is right.But the Problem is the way you print answer. See you'r last line in code.

this one cout << p << "\n" << suf[1] << endl;

My code is not expected to reach there cauz if it reached there then there is not such point possible, so I put that line for debugging purpose.
Also it is reaching the end in testcase 14.

roll_no_1

+16

The code given in the editorial for problem D seemed too complicated to me. So, I got the idea from the editorial and then read vntshh's solution which was very helpful to understand it. With the help of that, I wrote a commented solution for the problem. Here is the code, if you need any help: 42211321

eXCore

-41

Really?

You can replace the add(a, b) statements with (a + b) % mod, and it will still work. The functions are there just to avoid overuse of the % operation, as it is an expensive operation as compared to addition and subtraction. Further adding a lot of %s makes the code look messy.

Well, maybe modulo operation is just a little bit slower than addition and substraction, but, first of all, you do c = a + b when c is ll, but a and b are ints, so you have no profit of this thing. Also, in substraction, you even didn't changed the c's type. As of mult, it's even worse. You still using the % operator (so no boost in performance) and beside that, the multiplication itself is definitely wrong and would cause an overflow on big numbers(here it probably would not, because of the constraints, but if p would be p <= 10^10 consider multiplication a pair of these). My point is, if you wanna do it — do it right, or don't at all.

seven_triple

please explain solution of problem B

Considering the constraints of this problem, you just have to find 2 string(numbers) that alone would have max digit sums, but when added would have the minimum(1). So, a simple way to do this is just create 2 string (any way you want), when first string would be '9'*x + '0'*(x-1) + '1' and the second is just '9'*x. + is concatination, c*x is repeating x times char c. Why? Because when added they would result in '1' + '0'*(2*x-1), so the digit sum is one. X can be 1000 for example.

I didn't find any better alternatives for multiplications, so using mod. It won't overflow as multiplication is left to right associative, multiplication with 1ll converts it into a long long, and later the answer modulo 1e9+7, must be an int, so I return an int.
I use the sub operation when 0 <= a, b < mod. Note that a-b can not be <= -mod. So, even if it becomes negative, the absoute value of the result will never exceed mod-1, so adding mod converts the answer to a positive number. Furthermore, even if the answer is non-negative, it cannot exceed mod.
I accept that in c = a + b, c must have been an int. I wrote this function some time back, and not paying much attention to whether 2*(mod-1) (which is the max. value of a + b) will fit into an int or not, I took the result into a long long variable, but yes int will probably do in that case. So, Sorry for that.

-29

Yes, multiplication wont overflow considering a and b are ints. But, following today's "trends" you can see more problems involving modular arithmetics using the 64-bit ints, and then, your mult wont work. You can google for log n modular multiplication, if you are curious.
Modular substraction is a hell of the problem actually, try printing -6 % 5 in C++ and Python. And both solutions are logical.
Why do you even using ints, is it a try of getting performance boost? Cause I'm heard something about "slow 64-bit operations" but never seen a comparison. I've been using 64-bit ints and long doubles only and, till now, haven't experienced issues with that, instead i never think "should i put int, or long long this time?".

-23

Yeah, keep downvoting, show the codeforces' community actual face.

Pratyush1019

What is test 57 of problem E? My code is showing TLE on test 57 though its O(N). Here is the link to the code http://codeforces.net/contest/1028/submission/42212637

Aidos

test: 2 1 2

when j equal n-1, while(i != j) work infinitely

can anyone give better explanation for problem B.

Yinku2017

You can make another two strings to solve Problem B.

44444445+55555555=100000000

you can get shortest string a and b using this algorithm:

if(n<=5) a='5',b='5',n=0; so s(a)>=s(n) and s(b)>= s(n) and s(a+b)=1 well less or equal to any n. else { a='5',b='5',n-=5; while(n>=4) a='4'+a,b='5'+b,n-=4; }

because of when n-=4, s(a)+=4 and s(b)+=5, so it can ensure that s(n)<=s(a) and s(n)<=s(b).

rajg

I am getting heap buffer overflow in problem C while it runs fine on my computer. Can somebody check my code. 42215352

instead of cs* tmp = (cs*)malloc(sizeof(cs*)); you should write cs* tmp = (cs*)malloc(sizeof(cs));

It works. Thanks

SrapZark

In problem D, what is the reason for adding m + 1 instead of m in the answer for the undetermined directions of remaining orders?

If the values of the undetermined n ADD orders are v1, v2, ... vn (in ascending order), so in one possible assignment all of them can be sell orders, or the first one is buy and the rest are sells, or the first two are buys and the rest are sells, ...... or all of them are buys. These are n+1 possible assignments.

Asgar

Alternative solution for problem C:

Let x1, x2, and y1, y2 be the maximum two left x-coordinates and bottom y-coordinates of the rectangles, respectively. Then the answer is one of those four combinations, i.e. (x1, y1), (x1, y2), (x2, y1), (x2, y2).

deep_thinker26

What's the reasoning behind it?

First, there's such a point (x, y) that satisfies the condition (possible answer) and its x value is the x-value of some rectangle, and likewise y-value. (*)

WLOG, assume that x1 <= x2 and y1 <= y2. (These are the same values as I assumed in the above comment). Then if x < x1 or y < y1, then this point would not be in at least two rectangles, that's why it must be the case that x >= x1 and y >= y1. Combining this with (*) proves the statement.

Would it?

Spoiler

In this case, actually all four combinations can be the answer.

albeXL

+10

The solution to the problem http://codeforces.net/contest/1028/problem/C is almost the same as that of this problem http://codeforces.net/contest/1029/problem/C cool to have two consecutive rounds with similar problems.

Swistakk

-6

"Bonus: Solve the problem, if you need to find intersection of some n - k of n rectangles, if k ≤ 10."

I suppose it is very standard task to find a place where biggest number of rectangles intersect (no matter whether it is n-1, n-10 or 2137 for n=1e5). You simply sweep them from left to right with appropriate segment tree. It was given as a task on Polish OIG long ago which is contest for <=15 year old guys :P

Kostroma

+69

Come on man, it's not interesting. Better find a solution in O(nk²).

kakgucci

Seems, like the following works: Solve independent for X and Y. Every rectangle is just segment on axis X and the same for Y. Now we can easy find in O(N × log(N)) all X-es, which covered by at least n - k rectangles(now segments), there will be O(K) such x-es, after do the same for y and after that brute every such point in O(N). Is it ?

-28

Maybe it's not very interesting, but it seems like you guys missed it :D. Nevermind. Could you explain your solution? (I presume it is not solution mentioned here already 2 times since this one contains $\text{[math]}$ from sorting)

Lol, of course we didn't miss it)

Our approach is the following: the x-coordinate of the result will be either one of the k + 1 minimum right x-borders or one of the k + 1 maximum left borders. The same with y. So we have a solution in O(nk²), which is very easy and fast to write :)

MonsterInMe

can you explain for Case k = 2 ...

Hint: solve problem for segments first, not for rectangles. If all segments intersect, then the leftmost right border lies inside their intersection. So if you erase any two segments, others will intersect in one of the 3 leftmost right borders anyway, if they intersect at all, because in the worst scenario you erased these two segments which had two leftmost right borders.

I actually solved problem C with this approach, for k = 2.

Ali.Haidar

can we solve G without dp?can we say that dp(l,q)=((l+1)^q-l)

P0LyFish

In problem F, can you explain why number of points (x, y) with x^2 + y^2 = C is equal to the number of divisors of C after removing all the prime divisors of 4k+3 form?

_h_

I don't know if there's a natural bijection between divisors and positive solutions to x² + y² = C; but I know that both numbers are equal to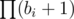 $\text{[math]}$ where b_i are the exponents in the prime factorisation of C (assuming all prime factors are of the form 4k + 1; other primes won't increase the number of solutions) (the formula is off by one if C is a square, because then there is a solution with y = 0 that is counted by $\text{[math]}$ ).

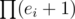Here's a sketch of how to derive the formula using Gaussian integers (they might seem scary, but I think the theory is also very beautiful):

First, note that N(x + iy) = x² + y² is a multiplicative function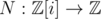 $\text{[math]}$ ; that is, N(z₁·z₂) = N(z₁)·N(z₂).

Second, recall that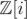 $\text{[math]}$ has unique factorisation; that is, any 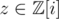$\text{[math]}$ can be uniquely expressed as a product of "Gaussian primes" and a unit (one of 1, i, - 1, and - i). (There is the slightly annoying fact that each Gaussian prime has 4 associates including itself, but really they are the same. You can avoid this annoyance by picking your favourite among the associates and only using that one for factorisations, like how, in 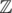$\text{[math]}$ , you might write - 15 = ( - 1)·3·5 instead of - 15 = 1·( - 3)·5; we prefer 3 over - 3.) Now since the norm is multiplicative, and units have norm 1, you can determine N(z) from the multiset of Gaussian primes in the factorisation of z. Since we want positive integer solutions, z = x + iy has to lie in the first quadrant, so we will always have 1 choice of unit for any given multiset (if C is a square, our formula also counts the solution with y = 0). So the number of solutions is the number of multisets of Gaussian primes such that the product of the norms is C.

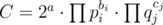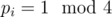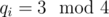Finally, we need the classification of Gaussian primes: each Gaussian prime either has norm 2 (only one such Gaussian prime), p = 4k + 1 ( two Gaussian primes for each p), or q² (q = 4k + 3) (only one Gaussian prime for each q). So the multisets are not too hard to count: If $\text{[math]}$ , with $\text{[math]}$ and $\text{[math]}$ , then the number of multisets is 0 if some c_j is odd, and 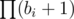$\text{[math]}$ otherwise. (The only choice is in how to choose the primes of norm p_i = 4k + 1: you need to distribute b_i among two Gaussian primes, so there are b_i + 1 possibilities.)

Also, I guess the limits on x, y were increased. The maximal number of solutions for C ≤ 2·112904² seems to be 196, which is achieved by C = 5²·13·17·29·37·41·53 = 12882250225. However, only 172 of the solutions have both coordinates ≤ 112904. For the record, here's a program that generates the points with unnecessary efficiency.

#include <bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i = a; i < (b); ++i)
#define trav(x,v) for(auto &x : v)
typedef long long ll;
typedef vector<int> vi;
typedef pair<int,int> pii;
typedef complex<ll> ci;

ll mexp(ll a, ll e, ll md){
	ll res = 1;
	while(e){
		if(e%2) res = res * a % md;
		a = a * a % md;
		e /= 2;
	}
	return res;
}

int root(int p){
	while(true){
		ll x = rand()%(p-3)+2;
		x = mexp(x, (p-1)/4, p);
		if(mexp(x, 2, p) == p-1) return x;
	}
}

ll norm(ci a){
	return (a*conj(a)).real();
}

ci quot(ci a, ci b){
	ci c = a * conj(b);
	ll r = norm(b);
	return ci( round(double(c.real())/r), round(double(c.imag())/r));
}

ci gcd(ci a, ci b){
	while(norm(b)){
		ci t = a -= b*quot(a, b);
		a = b;
		b = t;
	}
	return a;
}

int main(){
	vi ps = {5, 13, 17, 29, 37, 41, 53};
	vi es = {2,  1,  1,  1,  1,  1,  1};
	ll prod = 1;
	rep(i,0,7) rep(_,0,es[i]) prod *= ps[i];
	vector<ci> ga(7);
	rep(i,0,7){
		ll r = root(ps[i]);
		ga[i] = gcd( ci(ps[i], 0), ci(r, 1) );
		assert(norm(ga[i]) == ps[i]);
	}
	vector<ci> ls(1, ci(1,0));
	rep(i,0,7){
		vector<ci> nx;
		trav(w, ls) rep(k,0,es[i]+1){
			ci z = w;
			rep(_,0,k) z = z * ga[i];
			rep(_,k,es[i]) z = z * conj(ga[i]);
			nx.push_back(z);
		}
		ls = nx;
	}
	trav(z, ls){
		ll x = z.real(), y = z.imag();
		x = abs(x), y = abs(y);
		assert(x*x + y*y == prod);
		if(x > y && x <= 112904){
			cout << x << ' ' << y << endl;
			cout << y << ' ' << x << endl;
		}
	}
}

Wow, too much new knowledge. Thanks for your response!

vaibhav138

+18

For bonus task C :

Sweep only on x first, now one can prove that there will be at most 2*k + 1 points(while sweeping), where there are n-k rectangles above it. For each of these x sweep on y to find if there is a y that actually contains n-k rectangles.

Complexity O(n*k*logn);

2*k + 1 points because -> suppose I reach a x where there are n-k rectangles above on the subsequent points the number of rectangles may increase decrease or remain saim. In worst case it can form the pattern n-k, n-k+1, .. n , n-1, n-2 .. n-k.

Solution : 42217561

manish_joshi

For Problem C, You can use multiset to get O(n log n) with a simpler solution 42241507

1700 ms, using "n log n" solution. Let's see why.

No fast input.
Let's count log n operations actually. So we have 4 log n in input, so O(4*N log N). + 12 log n operations in computing intersections(notice the find() operations), so O(12*N log N). In result we have O(16*N log N). TYI, log2(10^5) ~= 17.
Summing up, your constant is almost as high as log N multiplier, which means, you have almost O(N log^2 N) solution.

I hope you understand that 300 ms is not that far from the TLE, so next time i suggest you to optimize your solutions.

Thank you for your details analysis !

I actually find that prefix and suffix array way(editorial) harder and ugly.(Maybe it's just me)

Well i added Fast IO to the same solution and got AC with 982 ms 42251111.

It's still far slower that this random submission of 180 ms i picked, 42249815.

But mine is much cleaner, you might agree.

Yeap, as for cleanness of code, definitely. As for time, of course, asymptotic is different, nothing surprising.

I wrote a very similar solution during the contest but with fast input and it passed in about 900 ms. But anyway it can be optimized by keeping track only of the maximum 2 and minimum 2 of bottom left x & y and top right x & y respectively. It will be O(N).

Tima

+39

For bonus C: X, Y can't be answer if we find k rectangles such that x2[i] < X, or if there exist k rectangles such that x1[i] > X. Similarly for Y. Let's sort x2, y2 in ascending order, x1, y1 in descending order. We get that x1[k] ≤ X ≤ x2[k], y1[k] ≤ Y ≤ y2[k]. Then check all possible 4·k² variants.

Solution: 42165553.

Xellos

+17

Phew. Solved G by casework, complexity O(4·10⁴) and even that comes from just building the query lists, all decisions are O(1). It goes like this:

If we're considering a range [m, M] with m ≥ 10⁴, the solution is just 10⁴ + 1-nary search, for which it's easy to calculate the maximum possible value of M - m + 1 given the number of remaining questions. Since we need to ask for at most one number until getting an answer > 0, the smallest possible value of the number in the first query is uniquely given: 204761410474.

The optimal 2-question strategy without the 10⁴ constraint is just to ask about 2m, 2(2m + 1), 2(2(2m + 1) + 1) etc., using as many numbers as we can, so that in the next question, we'd have at worst M = 2m - 1 and could ask about all numbers in the range [m, 2m - 1].

Let's assume we got answer 0, since this is the only interesting case. The next question is for some number x < 10⁴. Now, depending on the answer,

if the answer was 0 again:
- if the next answer is also 0, we're down to 2 questions, which must be for 2 and 1 or for 2 and (3, 4, 5), there aren't many options here
- this means the next number to ask about is 6 so that (3, 4, 5) would cover all remaining numbers
- if the next answer is 1, we have m = 7, can ask about 7 numbers and it's pretty clear that they need to be less than 10000, so the 2-question strategy says they should be 14, 30, 62, 126, 254, 510, 1022, with M ≤ 2045 so this could work
- in order to get M = 2045 in that case, the number we need to ask about in this question (the 2nd question) needs to be x = 2046
if the answer was > 0, then m = 2047 and M = 204761410473; there are 3 questions left
- since M is so large (much greater than 10⁸), the largest number to ask about must be y such that [y + 1, M] can be handled using the "over 10000" strategy described at the top
- this gives M - y ≤ (10⁴)(10⁴ + 1) + 10⁴ and optimally y = M - 10⁴(10⁴ + 2)
- the next smaller number must obey the same rule for y - 1, so it's M + 1 - 2(10⁴ + 1)², the next smaller number is M + 1 - 3(10⁴ + 1)² etc
- we can actually find all 2047 numbers this way, the last one is 20468427
- if the answer to the 3rd query with these numbers is > 0, it's the "over 10000" strategy again, so let's assume the answer is 0

Now there are 2 queries left, we have M = 20468426 and m = 2047 and there isn't much of a choice. Since the last query needs to contain up to 10000 consecutive numbers, the largest number must be 20468426 - 10000, the second largest 20468426 - 1 - 2·10000 etc. This way, we can find 2045 numbers, the last of which is 16382. There are 2 numbers left and they can be decided based on the 2-query strategy with small M: 2·2047 and 2(2·2047 + 1), which are 4094 and 8190.

As it turns out, if the answer is 2 now, we have m = 8191 and M = 16381, so M = 2m - 1, so this strategy proves that the bounds really are tight — the paths in the decision tree correspond to disjoint sets of answers.

The above is an excellent example of how NOT to solve programming problems.

RoronoaXoro

For problem C: Rectangles, is there a solution using convex hull technique? Can someone explain it to me.

In problem H, shouldn't it be relax best[k+dist] with dp[val][k] not dp[val][dist]?

RobeZH

I found a typo in the solution for Problem H, Before doing this for i, we need to update best array: for each val | ai and aival having dist primes in factorization and for each k≤7 relax best[k+dist] with dp[val][dist]. Then all queries with right border equal to i can be answered in O(Mans) time, where Mans≤14. We should relax best[k + dist] with dp[val][k] instead of dp[val][dist].

NguyenfromVN

I have a solution for C with O(n) and also for bonus problem with O(k*n). My submission: my_submission Initial result is 1st rectangle. I do a for loop from 2 to n and find intersecting rectangle of the result and each rectangle from 2nd to n-th. If intersecting rectangle is empty, I will skip this rectangle and dont include it in the result, but I keep it in an archive. When size of the archive is 2, it means I skip 2 rectangles and will have wrong result. Then, if this happen, I make sure that these 2 rectangles must be a part of the final result, so I break the for loop, do a for loop again from 1 to n with initial result is intersecting rectangle of 2 rectangles in the archive. Final result is initial rectangle after for loop. For bonus problem, I also use this technique with condition to break the first loop is the size of archive exceed k instead of 1. Then with each rectangle in k+1 rectangles in the archive, I will do a for loop from 1 to n and try to find valid result and stop when I get an valid one.

Блог пользователя Kostroma