Разбор
Tutorial is loading...
Решение (Vovuh)
n, k = map(int, input().split())
print((k + n - 1) // n)
Разбор
Tutorial is loading...
Решение (Vovuh)
q = int(input())
for i in range(q):
n, m, k = map(int, input().split())
if (n < m): n, m = m, n
if (n % 2 != m % 2):
k -= 1
n -= 1
elif (n % 2 != k % 2):
k -= 2
n -= 1
m -= 1
print(-1 if k < n else k)
Разбор
Tutorial is loading...
Решение комбинаторное (PikMike)
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
using namespace std;
long long C[20][20];
long long pw[4];
long long cnk(int n, int k){
if (k < 0 || k > n) return 0;
return C[n][k];
}
long long get(int n, int lft){
long long tot = 0;
forn(i, lft + 1)
tot += cnk(n, i) * pw[i];
return tot;
}
long long calc(long long x){
string s = to_string(x);
long long res = 0;
int cur = 3;
int n = s.size();
forn(i, n){
if (s[i] == '0') continue;
res += get(n - i - 1, cur);
--cur;
if (cur == -1) break;
res += get(n - i - 1, cur) * (s[i] - '1');
}
return res;
}
int main() {
forn(i, 20){
C[i][0] = C[i][i] = 1;
for (int j = 1; j < i; ++j)
C[i][j] = C[i - 1][j] + C[i - 1][j - 1];
}
pw[0] = 1, pw[1] = 9, pw[2] = 81, pw[3] = 729;
int T;
scanf("%d", &T);
forn(i, T){
long long L, R;
scanf("%lld%lld", &L, &R);
printf("%lld\n", calc(R + 1) - calc(L));
}
return 0;
}
Решение прекалком (PikMike)
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
using namespace std;
vector<long long> res;
void brute(int pos, int cnt, long long cur){
if (pos == 18){
res.push_back(cur);
return;
}
brute(pos + 1, cnt, cur * 10);
if (cnt < 3)
for (int i = 1; i <= 9; ++i)
brute(pos + 1, cnt + 1, cur * 10 + i);
}
int main() {
brute(0, 0, 0);
res.push_back(1000000000000000000);
int T;
scanf("%d", &T);
forn(i, T){
long long L, R;
scanf("%lld%lld", &L, &R);
printf("%d\n", int(upper_bound(res.begin(), res.end(), R) - lower_bound(res.begin(), res.end(), L)));
}
return 0;
}
Разбор
Tutorial is loading...
Решение (Ajosteen)
#include <bits/stdc++.h>
using namespace std;
const int N = 300 * 1000 + 9;
int n, m;
int a[N], b[N];
int main() {
scanf("%d", &n);
for(int i = 0; i < n; ++i) scanf("%d", a + i);
scanf("%d", &m);
for(int i = 0; i < m; ++i) scanf("%d", b + i);
long long sum = 0;
for(int i = 0; i < n; ++i) sum += a[i];
for(int i = 0; i < m; ++i) sum -= b[i];
if(sum != 0){
puts("-1");
return 0;
}
int posa = 0, posb = 0;
int res = 0;
while(posa < n){
++res;
long long suma = a[posa++], sumb = b[posb++];
while(suma != sumb){
if(suma < sumb) suma += a[posa++];
else sumb += b[posb++];
}
}
printf("%d\n", res);
return 0;
}
Разбор
Tutorial is loading...
Решение (PikMike)
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
using namespace std;
const int N = 1000 + 7;
struct seg{
int x1, y1, x2, y2;
seg(){};
};
struct line{
long long A, B, C;
line(){};
line(seg a){
A = a.y1 - a.y2;
B = a.x2 - a.x1;
C = -A * a.x1 - B * a.y1;
};
};
int n;
seg a[N];
int get(seg a){
int dx = a.x1 - a.x2;
int dy = a.y1 - a.y2;
return __gcd(abs(dx), abs(dy)) + 1;
}
long long det(long long a, long long b, long long c, long long d){
return a * d - b * c;
}
bool in(int x, int l, int r){
if (l > r) swap(l, r);
return (l <= x && x <= r);
}
bool inter(seg a, seg b, int& x, int& y){
line l1(a), l2(b);
long long dx = det(l1.C, l1.B, l2.C, l2.B);
long long dy = det(l1.A, l1.C, l2.A, l2.C);
long long d = det(l1.A, l1.B, l2.A, l2.B);
if (d == 0)
return false;
if (dx % d != 0 || dy % d != 0)
return false;
x = -dx / d;
y = -dy / d;
if (!in(x, a.x1, a.x2) || !in(y, a.y1, a.y2))
return false;
if (!in(x, b.x1, b.x2) || !in(y, b.y1, b.y2))
return false;
return true;
}
int main() {
scanf("%d", &n);
forn(i, n)
scanf("%d%d%d%d", &a[i].x1, &a[i].y1, &a[i].x2, &a[i].y2);
int ans = 0;
int x, y;
forn(i, n){
ans += get(a[i]);
set<pair<int, int>> pts;
forn(j, i)
if (inter(a[i], a[j], x, y))
pts.insert({x, y});
ans -= pts.size();
}
printf("%d\n", ans);
return 0;
}
1036F - Relatively Prime Powers
Разбор
Tutorial is loading...
Решение (PikMike)
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
using namespace std;
const int K = 100;
const int N = 100 * 1000 + 13;
const long long INF64 = 3e18;
int mu[K];
void precalc(){
static bool prime[K];
static int lst[K];
memset(prime, false, sizeof(prime));
forn(i, K) lst[i] = i;
for (int i = 2; i < K; ++i){
if (lst[i] == i) mu[i] = 1;
for (int j = 2 * i; j < K; j += i){
lst[j] = min(lst[j], lst[i]);
if (lst[j] == lst[i])
mu[j] = 0;
else
mu[j] = -mu[i];
}
}
}
int mx[K];
long long binpow(long long a, int b){
long long res = 1;
while (b){
if (b & 1){
if (res < INF64 / a) res *= a;
else return INF64;
}
if (b > 1){
if (a < INF64 / a) a *= a;
else return INF64;
}
b >>= 1;
}
return res;
}
long long calc(long long n){
int pw = 63 - __builtin_clzll(n);
for (int i = 3; i <= pw; ++i){
if (mu[i] == 0) continue;
while (binpow(mx[i], i) > n)
--mx[i];
}
long long res = n - 1;
for (int i = 2; i <= pw; ++i)
res -= mu[i] * (mx[i] - 1);
return res;
}
int get_sqrt(long long n){
int l = 1, r = 1000000000;
while (l < r - 1){
int m = (l + r) / 2;
if (m * 1ll * m <= n)
l = m;
else
r = m;
}
return (r * 1ll * r <= n ? r : l);
}
long long ans[N];
int main() {
precalc();
int T;
scanf("%d", &T);
vector<pair<long long, int>> q;
forn(i, T){
long long n;
scanf("%lld", &n);
q.push_back({n, i});
}
sort(q.begin(), q.end(), greater<pair<long long, int>>());
mx[3] = 1000000;
mx[4] = 31622;
mx[5] = 3981;
for (int i = 6; i < K; ++i)
mx[i] = 1000;
forn(z, T){
long long n = q[z].first;
mx[2] = get_sqrt(n);
ans[q[z].second] = calc(n);
}
forn(i, T)
printf("%lld\n", ans[i]);
return 0;
}
Разбор
Tutorial is loading...
Решение (BledDest)
#include <bits/stdc++.h>
using namespace std;
const int N = 1000043;
vector<int> g[N];
vector<int> gt[N];
vector<int> src;
vector<int> snk;
int reach[20];
int used[N];
void dfs(int x)
{
if(used[x]) return;
used[x] = 1;
for(auto y : g[x]) dfs(y);
}
int main()
{
int n, m;
scanf("%d %d", &n, &m);
for(int i = 0; i < m; i++)
{
int x, y;
scanf("%d %d", &x, &y);
--x;
--y;
g[x].push_back(y);
gt[y].push_back(x);
}
for(int i = 0; i < n; i++)
{
if(g[i].empty())
snk.push_back(i);
if(gt[i].empty())
src.push_back(i);
}
int cnt = src.size();
for(int i = 0; i < cnt; i++)
{
memset(used, 0, sizeof used);
dfs(src[i]);
for(int j = 0; j < cnt; j++)
if(used[snk[j]])
reach[i] ^= (1 << j);
}
bool ok = true;
for(int mask = 0; mask < (1 << cnt); mask++)
{
int res = 0;
for(int j = 0; j < cnt; j++)
if(mask & (1 << j))
res |= reach[j];
int cnt1 = __builtin_popcount(mask);
int cnt2 = __builtin_popcount(res);
if(cnt2 < cnt1 || (cnt2 == cnt1 && cnt1 != 0 && cnt1 != cnt))
ok = false;
}
if(!ok)
puts("NO");
else
puts("YES");
}










I found a strange thing in F. Two ACs codes output different result. Detail in https://codeforces.net/blog/entry/61728. Can anyone help me?
Can someone prove the author's solution for B?
i thought about this problem lot after the contest.
what i came up with is that there is 8 cases for m,n,k: odd/odd/odd, odd/odd/even....even/even/even. all cases reduce down to the odd/odd/odd case or the even/even/even case. we can see that it is possible to solve the odd/odd/odd or even/even/even case using all diagonal moves as long as m,n is reachable in k moves.
for an example of "reduction", the even/odd/odd case reduces to the even/even/even case because you can "spend" one non-diagonal move in the n-direction. [1]
the author's solution is basically "reducing" down all cases to o/o/o or e/e/e cases with mod. see my coded sol here: 42690270
[1] in fact, the o/o/o case reduces down to the e/e/e case by spending 1 diagonal move
Randomized solution for problem G: here
cool.
I will try to explain why this solution works: obviously (unless I missed some bug of course, but from conceptual standpoint the solution seems pretty sound), the solution in question can make only one type of mistake: answer "YES" when the actual answer is "NO".
When the answer is "NO"? When there is at least one "bad" permutation of numbers from 1 to k. I will show that in this cases there are actually a lot more bad permutations than just one. Indeed, consider the set X from the editorial.
To explain the main idea lets consider the simplest case when |X| = |f(X)|. Then any permutation that matches elements of X only with elements of f(X) and matches elements {1, 2, ..., k} - X with elements {1, 2, ..., k} - f(X) is a bad permutation: when doing a graph walk starting with some source in X, we will never leave reach any source not from X. Therefore there is at least |X|!(k - |X|)! ≥ [k / 2]![(k + 1) / 2]! bad permutations.
To deal with the case |f(X)| < |X|, we will take some subset Y of X with size |f(X)|, then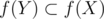 and we can similarly show that all permutations that match sources from Y to sinks in f(X) and sources not from Y to sinks not from f(X) are bad permutations. Therefore there is at least |Y|!(k - |Y|)! ≥ [k / 2]![(k + 1) / 2]! bad permutations.
and we can similarly show that all permutations that match sources from Y to sinks in f(X) and sources not from Y to sinks not from f(X) are bad permutations. Therefore there is at least |Y|!(k - |Y|)! ≥ [k / 2]![(k + 1) / 2]! bad permutations.
All in all, if there is one bad permutation, there are at least [k / 2]![(k + 1) / 2]! of them. So the probability of finding a bad permutation randomly is at least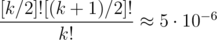 in the worst case of k = 20. From the other hand, on my computer, the code in question checks
in the worst case of k = 20. From the other hand, on my computer, the code in question checks 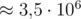 random permutations before timing out. In the end, the probability of failure is something of the order ≈ 10 - 8, which is good enough.
random permutations before timing out. In the end, the probability of failure is something of the order ≈ 10 - 8, which is good enough.
cool
Wasted 1 hour trying to solve a harder version of Problem C. I thought classy numbers were those number which had the number of distinct non zero digits <= 3. And when TC 2 and 3 were not passing, I tried so hard debugging.
After successfully wasting 1 hour, read the question again and BAM!!
The data for G maybe too weak? I can easily hack my code.
The problem A is so easy, but I solved it late because of my poor English and my poor wi-fi.
In problem E, Can anyone please give proof of why exactly GCD + 1 value will give integer co-ordinates?
Spoiler
Thanks ^_^
[Deleted]
In Problem G, it is possible to find for every sources all achievable sinks in a linear time. For this it is necessary to store in each visited vertex an integer (the set of bits of achievable sinks).
Can problem F be solved with some precalculations (generations of correct numbers), simular to problem C?
there is a easy way to solve problem C with DP :) 42742195
It seems to be an interesting approach, but I don't really understand it. Could you please explain it briefly?
f(i,j)means The i th bit of a number(unit's digit,ten's digit...) and already has j non-zero digits.DP uses
flagto control upper bound.If it is not the upper bound,we can remember the result off(x,y).(That's why I initializefto -1 and updatef(x,y)when flag=0).f(x,y)will be accessed multiple times, so we can speed it up by remember it .My English is poor( I use the google translate QAQ ).
Why dont we use -C instead of C? I read in internet that the formula will use -C instead of C? I mean this fragment: long long dx = det(l1.C, l1.B, l2.C, l2.B); long long dy = det(l1.A, l1.C, l2.A, l2.C);
By the properties of determinant
det(-a, b, -c, d) = det(a, -b, c, -d) = -det(a, b, c, d)Ahh it is used then when he does: x = -dx / d; y = -dy / d; right?
Why is Problem A tagged with FFT ? Is there a solution with FFT as well ?
Nope, it means an idiot is going around and trolling.
very very good~ !!
E has a tag "fft". Can it be done using FFT too? If yes, then how?
Honestly, do you even know how to use FFT in the first place?
I do. I'm looking for more questions to practice it.
For problem 1036E — Covered Points , can anybody explain what's special with the test 14? I've seen some people failing this test.
Could someone explain how mobius function could be used in problem F. All I understood is that we are trying to remove the bad elements from the answer. Basically, could someone explain me the formula?
in problem G, how about a 4-vertex graph: 1->2, 3->2, 3->4 ??? It's obvious that 1 is a source but the set of sink it can reach is just {2}???
is there a proof for problem b ?
Can someone explain the brute force generation for C
pos represents the number of digits,cnt represents count of non-zero digits and cur represents the value generated. first we take the generated number and multiply by 10 and increasing number of digits. if a number is classy number then its multiple of 10 will also be a classy number. then we check if the number has less than 3 non-zero digits or not.if it has less than 3 non-zero digits then we can put any number between 1 to 9 at units place and generate another classy number(multiply by 10 and adding the number). we also increase the count of non-zero digit.
I was really confused. thanks for the explanation.
Why it is TLE for Test-Case #23 code B'coz complexity is O(N + M)
please can anyone explain the formula in problem C, i dont know why it return exactly the beautiful numbers on [1,X), why cur-- like that, that means for(int cur = 3; cur>=0; cur --) , i think i'll insert s[i] in a set so that its size is cur ... A lot of things i cant understand. I've read PikMike's code and the formula for hours. Help me please.
Proof why GCD works in E
The solution to G reminds me of Hall's marriage theorem, and I finally figured out how to solve it in polynomial time.
Take the graph of sources and reachable sinks. If no perfect matching exists, by Hall's marriage theorem, there is a nonempty proper subset of sources $$$X$$$ such that $$$|X|>|f(X)|$$$, so the answer is NO. Otherwise, we need to ensure that $$$|X|<|f(X)|$$$. This means $$$f(X)$$$ has sinks besides the ones matched to sources in $$$X$$$. Connect each sink to the source it is matched to in the perfect matching. The answer is YES if and only if the the resulting graph is strongly connected.
Code: 67053099
Can anyone explain F with little more details ?