back_slash's blog

Question on Prime Factorization
By back_slash, history, 6 years ago, In English

You are given two natural numbers N and K. You need to represent the number N as a product of K numbers such that all the K numbers are >= 2 and the sum of the K numbers is minimum. The constraints on the value of N <= 10^12. Given such values of K for which the answer always exist.

My Solution:- After finding the prime factorization of the number N. Insert the factors in a multiset and then solve the problem greedily. Take the first 2 elements of the multiset, remove them and then insert their product in the multiset. Keep on repeating this process until the size of multiset becomes equal to K.

I don't know whether the above approach is correct or not and also I am not sure whether the answer will be unique or not.

Any suggestions for the given approach or some new approach are welcomed.

UPD:- I know my approach is incorrect but still I am unable to figure out anything about uniqueness. Whether the answer will be unique or not.

  • Vote: I like it
  • +11
  • Vote: I do not like it

»
6 years ago, # |
← Rev. 4   Vote: I like it +31 Vote: I do not like it

Your solution is wrong; take N = 36, K = 2.

You can solve the problem in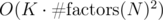 with DP.

EDIT: This might be too slow, depending on the test data.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    Thanks for the reply!!! Can we say anything about the uniqueness of the K numbers?? If we take the numbers in sorted order will the answer be unique?

    → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by back_slash (previous revision, new revision, compare).

→ Reply