| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
Given an array A consist of N integers (N <= 100000, 0 <= Ai <= sqrt(i) for 1 <= i <= N). Count the number of triple (i, j, k) such that i <= j <= k and (Ai xor Aj xor Ak) = 0.
I tried many approaches but I couldn't optimize my O(N^2) solution. Is there any efficient algorithm to solve this problem?
We can improve complexity to
due to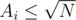 
. Calculate frequencies of the elements while going from left to right, considering the Ak element in the triple. Now, we need to find the number of pairs i, j such that 
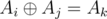. Now, in 
time we can traverse the frequencies, considering element Aj, assuming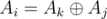 
, and adding freqAj × freqAi for Ai < Aj (that way we will count each pair once). Case of Ak = 0 should be handled separately — 
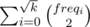. The actual running time will be slightly better than 
since we don't traverse all the frequencies every iteration.