Credits:
Div2A (Make a Trianle): Idea by Zlobober, development by vintage_Vlad_Makeev
Div2B (Equations of Mathematical Magic): Idea and development: Glebodin
Div1A (Oh Those Palindromes): Idea by Endagorion, development by Andreikkaa
Div1B (Labyrinth): Idea and development by qoo2p5
Div1C (Dwarves, Hats and Extrasensory Abilities): Idea and development by mingaleg
Div1D (Candies for Children): Idea by Endagorion, development by Flyrise
Div1E (Lasers and Mirrors): Idea and development by mingaleg
Div1F (String Journey): Original idea by GreenGrape,  solution by vintage_Vlad_Makeev, development vintage_Vlad_Makeev and GreenGrape
solution by vintage_Vlad_Makeev, development vintage_Vlad_Makeev and GreenGrape
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...










D: I think the first part should be O(n). It is quite easy.
yes
.
Can anyone explain me intuition behind DIV2 B? I did not understand the tutorial that clearly? Thanks in advance !!:)
Try looking yourself how they behave on some examples, like a = 3, a = 2 and some reasonable x's.
A claim is that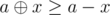 (always) and equality holds if and only if bits of x form a subset of bits of a.
(always) and equality holds if and only if bits of x form a subset of bits of a.
a^x = a + x — 2 * (a & x) [ XOR property]
So, a^x = a-x => a + x — 2 * (a & x) = a — x => a & x = x
So, this is true when we take any subset of ones (set bit) of 'a' => ans = (1 << (cnt of set bit in a))
But wouldn't that give you some duplicate values? Like 100, hm can have abusers 0 and 00 which are the same.
Regarding Div2B, another method to solve: Rewriting the equation we have:
a = (a^x) + x
Now use the property x+y = (x^y) + 2*(x&y) , where ^,& are bitwise xor,and respectively.
Now the equation becomes:
a = (a^x^x) + 2(x&(a^x))
=> a = a + 2(x&(a^x))
=> x&(a^x) = 0
=> x&(!a) = 0 (Using a^x = ((a&!x) | (!a&x)))
Hence we have bits of x should be a subset of a, hence number of solutions are 2^t where t is the number of set bits in a
In Div2 D , Can someone explain why it can't use general bfs?
Thank you!!
Consider we are now at (i,j).If the problem doesn't have the limit about move left and right,It's just a simple bfs problem.
With limit,if one point can be reached by move (left,right) with many different ways, it is obviously that using less (left,right) move is optimal,because it maybe can reach more points.
So we can just use bfs to record the less (left,right) move.
See My Code 44337946
in your code i saw that you have put the condition that the sum of left and right moves should be low to maintain the order of the priority queue , but the editorial says its sufficient to minimize either of the left or right moves and i actually did this but got a WA , can you explain why its wrong ?
Just using simple bfs , move down or up with affect the order about move left and right
See this sample from ez_zh
20 7
3 6
5 2
......*
.****.*
.****.*
....*.*
..*
..*
..*
..*
..*
..*
..*
..*
..*
..*
..*
..*
..*
..*
**....*
*******
47
Sample, not simple.
Because the fastest way to reach some block from the starting block may exceed the left and right constraints.
Because there are two kinds of edges.(i.e. Which costs zero and which costs one).So when you are doing bfs, you need to insert a node in the front of the queue if its dist equals to the previous dist,and insert in the back if its dist equals to the previous dist plus one. You can also use dijkstra by heap optimize or Bellmen-ford by queue optimize. Sorry for My poor English.:)
Why this code 44315121 is getting runtime error? Question Div2.C.
That's div 2 C. You are a div 2 participant.
That is the same question,however I changed my comment.Thank you.
I've come up with a different approach for Div.1 D which runs in time, using the fact that
time, using the fact that  has at most
has at most 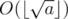 possible values, if both a and b are integers.
possible values, if both a and b are integers.
Proof:
If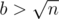 ,
, 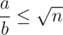 , which has at most
, which has at most  different values.
different values.
Otherwise, b has at most different values.
different values.
Lets call the number of taken candies of a single round num, which is n plus the number of people with a sweet tooth. Our purpose is to maximize num. To do this, we can check a bunch of num with same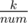 , which we'll call it r later, in the same time. Also, we'll call the number of children who took candies one more time than the others x, and k - r·num rem.
, which we'll call it r later, in the same time. Also, we'll call the number of children who took candies one more time than the others x, and k - r·num rem.
Here are the constraints for num:
Constraint 1 and 2 ensures the validity of r, constraint 3 ensures the validity of num, and constraint 4 and 5 ensures that there are enough space for children with a sweet tooth.
We can use some simple math to deform these constraints so that num will appear at only one side of the inequation.
Here's the original version: 44345319
Here's the trimmed version so that it was the shortest on 2018-10-15: 44345626
Some questions:
In definition of rem, did you mean k - r·num instead of k - r·sum?
Given that there may be someone with a sweet tooth in x, why the 4th inequation isn't 0 ≤ rem ≤ 2x?
What does the 5th inequation mean? I can't understand it.
Thanks in advance.
Yes, it was a typo. Thanks for pointing out.
Because at least x candies were taken out by x people.
num - n - min(rem - x + 1, x) is the number of people with a sweet tooth other than the x people.
Thanks for explanation. But I got confused when I looked into your code. The following inequation is used in your code:
And the result conflicts with the 4th inequation you mentioned above. Do I misunderstand something in your code?
Another question: in num - n - min(rem - x + 1, x), why we need +1 to rem - x? Just because the case where the last people with a sweet tooth?
Sorry, I think the fourth in-equation should be x ≤ rem ≤ 2x.
Reply to the second question: Because the last person may have a sweet tooth even if he took only 1 candy.
Div 2 C
Note that each palindrome have equal character at their ends. Suppose this character is c with x number of occurences. Then there are at most x(x+1)/2 palindromes with this character.
Can someone elaborate this. How did we get 1+2+...+x if c has x number of occurences?
Since 'c' has x number of occurrences, thus palindrome with 'c' are x , palindrome which are 'cc' are x-1 , palindrome which are 'ccc' are x-2 and so on.
so we get x+x-1+....+2+1 = x(x+1)/2 for 'c' which has frequency x.
Your explanation is not correct. You are counting number of palindrome substrings of string 'cccc..' lengh x. If we have x characters 'c', then we can choose x * (x — 1) / 2 pairs of characters 'c' to be head and tail of a substring, or we can choose x substring "c", so in total we have x * (x + 1) / 2 ways to choose a substring which may be a palindrome substring. That why x * (x + 1) / 2 is the upper bound.
I think you misunderstood my explanation, I am saying that we have x ways to choose a substring "c", x-1 ways to choose a substring "cc", x-2 ways to choose "ccc" and so on till we have 1 way to choose "ccc.. (x times) ".
so we get x+x-1+x-2+...+1 = x(x+1)/2
I mean your explanation didn't show how to get the upper bound. You was counting number of substrings of string "cccc..." length x, and be cause there is only one charater 'c', so they were also palindrome substrings. The result you got was of the case when the upper bound was satisfied.
Yeah, you wasn't wrong. Maybe i'm understanding the question in a different way
Can anybody help me why this code(Div-2 D) is giving WA 44323380
Why this code is not working, please point out the error (Div-2 D) CODE
4 5 4 2 1 2 ...** .*... .***. .....
Correct ans: 10. Your bfs will reach 2,3 but not with minimum left or right moves. That's why simple bfs with all edge weights same won't work as moving more up and down is feasible rather than moving left or right.
Tutorial for Div2-A(1064A) has an error, answer should be max(0,c-(a+b)+1) instead of max(0,c-(a+b+1)) where c = largest side of given triangle.
Fixed it, thanks.
For question F The way I see the fastest code is this: Use dp[i] to end the longest trip with i We insert all the suffixes of the last string (just dp[i]) into the hash table from long to short. If a string is inserted, stop inserting (the shorter suffix has already been inserted) So when we query whether the journey of the length r-l+1 ending in r (string [l, r]) is legal Just need to query whether [l, r-1] and [l+1, r] appear in the hash table. This does not require a suffix data structure, but I want to know what the time complexity is? O(n^1.5) or O(n)?
I think I have a proof for O(n). Assume that the dp is from left to right and dp[i] = length of the longest trip ending at i.
Let S(i) be the set of the smallest dp[j] substrings ending at j for each j from 1 to i. Let c1(i) be the number of distinct strings of the set S(i).
Call an index i type A if the second last string of the trip ending at [i-dp[i]+1, i] is equal to [i-dp[i]+1, i-1] and type B if it is [i-dp[i]+2, i].
It seems that c1(i) <= 2*i-dp[i+1]+O(1) (O(1) is some constant that I'm too lazy to find). We'll proceed by induction.
Case 1: i is type A and i+1 is type A
Since i+1 is type A, there is an occurrence of the string [i+1-dp[i+1]+1, i] before i+1-dp[i+1]+1. Thus, the substrings [i+1-dp[i+1]+1..i, i] do not contribute to c1(i), so c1(i) <= c1(i-1)+(i+1-dp[i+1]+1)-(i-dp[i]+1) <= 2*(i-1)-dp[i+1]+1+O(1).
Case 2: i is type A and i+1 is type B
Similar argument to Case 1, c1(i) <= 2*(i-1)-dp[i+1]+2+O(1).
Case 3: i is type B
Only [i-dp[i]+1, i] can be a new distinct string and dp[i+1]-1 <= dp[i], so c1(i) <= c2(i)+1+dp[i]-dp[i+1]+1 <= 2*(i-1)+2-dp[i+1]+O(1).
I understand. Cool proof!
In Div2 D / Div1 B
R - L = j1 - j0 = const But it can be written this way L — R = j1 — j0 = const
If we optimise any one of L and R, How to count the number of moves for another one at any (i, j) which equation of the above two should we use ? I am getting correct answer for equation R — L = j1 — j0 if i am consdering cost 1 for left move and 0 for other moves. why is that ?
Can someone explain how a+b is linear with respect to t in 1063D?
Actually we treat t as a constant, and a+b is parametric of z.
Now we just have to say the parametric
a = a0 + (t+1)z
b = b0 + tz, z is element of integers
is a line.
Solve for z = (a-a0)/(t+1) = (b-b0)/t
Since t, a0, b0 are constants this is actually just point-slope form of a line. (slopes are 1/(t+1) and 1/t)
Why can't we use a simple DFS in Div2D? It gives wrong answer on test 13. Here is my submission
let, describe each cell as a struct { row, col, leftCount, rightCount }
assume, you have a visited cell C and your current cell is CC;
where (CC.row == C.row) and (C.col == CC.col+1)
if(C.rightCount>(CC.rightCount + 1) || C.leftCount>CC.leftCount){
you have to call dfs with cell C again; why? because, now C has lesser leftCount or rightCount than before....so it may able to visit more cells than before} here is my code with bfs https://codeforces.net/contest/1064/submission/44414320
I did the same to you.
Div2 E / Div1 C
Is following approach right??
initially b=1 , w = n+2
if (white) print (b++, 1) ;;
else print (w++, 1) ;;
line -> (n+1,0) — (n+1,3)
and why i'm getting "idleness limit exceeded on test 1" ??
https://codeforces.net/problemset/submission/1064/44428642
Thanks in advance.
You are supposed to give the interactor the position of point first, and then the interactor would tell you the color.
OH!...Thanks. I never solved this type of problem!
In Div2 C editorial, it is written that, It is easy to see, that the sorted string fulfills that bound Would anybody explain me it, please? I do not understand this.
The way I like to think of it is trying all size "windows" on a single letter.
So imagine we have the string
a .... a .... a .... a where a's are evenly spaced out
In the optimal solution, the whole string is a palindrome and this satisfies the window of size 4. For example: abababa. Maximum there is 1 such window.
Now lets look at window of size 3. We need [a ... a ... a] to be a palindrome. There are maximum of 2 such windows.
Eventually we get 1+2+...cntA windows where cntA = amount of a's in the string.
Each letter should contribute 1+2+3...cnt = (cnt)(cnt+1)/2 palindromes in an optimal solution.
It is easy to see that a sorted string will always be optimal, because this property holds true. Actually any solution that "bunches" same letters together is optimal, so you can have ab O(n) solution (counting sort idea)
In Div2-D why This Code fails but This Code passes. According to editorial minimizing either of L or R should work but if this is the case then the former code should not give WA verdict on test 20. What am I missing here?
Handle the case where l or r hits negative (they are invalid)
l and r will always be positive because i am checking l>0 r>0 before pushing them in deque. Check out this. It gives WA not Runtime error. So l or r are always >= 0
It only confirms the node you are on meets this condition, not the neighbors you mark
Actually the same code passes Test case 20 if i use queue instead of deque. Link
since the current node has l>0 and r>0 and in one move they can be only decreased by one so l>=0 and r>=0.
It would be great if you could provide any test case on which my code with deque fails?
It's still incorrect if l > 0 and r > 0 you will only go to l=1,r=0 and l=0,r=1 cases, and miss the cases where l = r = 0
The fact that queue passes 20 just means it happens to work in the test case, not that it is any more "correct"
Ok I just edited yours a resubmitted, http://codeforces.net/contest/1064/submission/44520194
The l > 0 and r > 0 thing you said isnt even true, so you still have to fix the original issue of confirming the neighbors work
Thanks brdy. I solved the issue and got it accepted.
The issue was with my implementation of 0-1 bfs. 0-1 bfs generally involves relaxing edges but here when I was processing a node I was immediately marking its neighbours visited without considering the fact that since there may be more elements with the same L value in the queue there might exist a better path.
Correct output:53
My output was 52 on this case as both (3,8) and (10,1) nodes will have L value 1 but since (3,8) entered the queue first it will mark (3,7) while there exists a better path from (10,1).
Why does it surprise me that solution for interactive problem is binary search?
For Div 1 D, since first part can be done in O(n), binary search on number of sweet tooth in second part also pass the TL. ( O( min( n, (k / n) * log(n) ) ) ), about 2e6 operations.
For b, in div2, if a is 100, then the 2 subsets 0 and 00 are the same number right? So wouldnt the 2^k subsets have duplicate vakues?
In div2 D, I didn't understand how 1-2 bfs is used to minimize the number of left and right moves used to reach a position. Can someone please explain
You are doing a 0-1 BFS where each (i,j) is connected to up to 4 neighbors, with cost of vertical edges being 1 and cost of horizontal edges being 0. This means that at the end of the search, costTo[i][j] = numLeftsUsed+numRightsUsed.
Now since you are starting in column c and ending in column j, you must have numRightsUsed-numLeftsUsed = j-c. For instance if you start in column 1 and end in column 3, you might have used 0 lefts and 2 rights, or 1 lefts and 3 rights, or 2 lefts and 4 rights, etc.
This lets you solve for costTo[i][j] in terms of just numLeftsUsed or numRightsUsed:
numRightsUsed=j-c+numLeftsUsed so costTo[i][j] = numLeftsUsed + j — c + numLeftsUsed and similarly for expressing in terms of just numRightUsed.
Minimizing costTo[i][j] = numLeftsUsed+numRightsUsed = j-c+2*numLeftsUsed is equivalent to minimizing numLeftsUsed.
with 0-1 bfs, shouldn't you take horizontal edges with weight 1 instead?
In,div2D,why this code is getting TLE?? https://codeforces.net/contest/1064/submission/85460883
DIV2 D -->
just look at this solution :: you will understand https://codeforces.net/contest/1064/submission/107079705
Can somebody please tell me why am i getting TLE at test case 8 in my submission for Div.1 B question https://codeforces.net/contest/1063/submission/216168661 this is the link for my submission, i am doing a bfs traversal and with up down wights as 0 and left right weights as 1, thanks for your help
Can anyone please explain why this O(nmlog(nm)) submission TLEs? I just minimized R value for the left portion of the starting cell and separately minimized the L value for the right portion of the starting cell. 273341769