MikeMirzayanov's blog

2018-2019 ICPC, NEERC, Southern Subregional Contest (Online Mirror, ACM-ICPC Rules, Teams Preferred)
By MikeMirzayanov, 6 years ago, translation, In English

Hello!

ACM-ICPC Southern Subregional Contest (NEERC/Northern Eurasia) 2018 has ended on October 16. There were 72 teams onsite in Saratov, most of them were invited because of their result on the qualification stage.

On Oct/20/2018 11:05 (Moscow time) will start online-mirror 2018-2019 ICPC, NEERC, Southern Subregional Contest (Online Mirror, ACM-ICPC Rules, Teams Preferred).

In this contest I play a role of Cheif Judge and the jury teams consists of ex-participants of ICPC from Saratov and jury members from other cities. Many thanks to all of them! I hope you will like the problems!

I invite ACM-ICPC teams and individual participants of Codeforces competitions to take part! Sure, the contest will be unrated.

MikeMirzayanov

  • Vote: I like it
  • +221
  • Vote: I do not like it

Comments Comments (68)
| Write comment?
»
6 years ago, # |
  Vote: I like it +25 Vote: I do not like it

you forgot to thank MikeMirzayanov

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Will there be problems of all dificulties or just really tough ones?

→ Reply
»
6 years ago, # |
  Vote: I like it +6 Vote: I do not like it

Why some participants' number in the Registrants list is red?

→ Reply
»
6 years ago, # |
← Rev. 3   Vote: I like it -42 Vote: I do not like it

...

→ Reply
»
6 years ago, # |
  Vote: I like it -30 Vote: I do not like it

Is it rated? I'm serious.

→ Reply
»
6 years ago, # |
  Vote: I like it +71 Vote: I do not like it

How to solve M?

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I found out you have solved it, could you share the solution of M. QAQ

    → Reply
»
6 years ago, # |
  Vote: I like it +22 Vote: I do not like it

How to solve A?

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 7   Vote: I like it +43 Vote: I do not like it

    BFS. State: remainder, digit sum, number. Then, apply bfs. For every node, we can get its adjacent nodes like this, number * 10 + i, for their states, we can calculate remainder = (current node's remainder * 10 + i) % d and digit sum = (current node's digit sum + i) where i = 0 to 9. Then check for a particular node, if its remainder = 0 and digit sum = s, so this is our answer. For reference, my code: http://codeforces.net/contest/1070/submission/44598713

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      How did you get the intuition for this question? I mean, how did you came to conclusion that applying BFS would be good?

      Thanks for the summary.

      → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +1 Vote: I do not like it

      But how can we know the answer is '-1'? And why is BFS better than DFS?

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        In general, we are doing BFS because we want to find answer with minimum number of digits. (The intuition is that we want to go wide, not deep.)

        We visit all numbers who's digit sum is at most S. If we haven't found the number yet, the number doesn't exist :)

        → Reply
»
6 years ago, # |
  Vote: I like it +9 Vote: I do not like it

In J, is it just that only one character needs to be split across two sides and rest all characters will be only on one of the sides and rest do with bitsets?

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    Yes, but bitsets are too slow because of multitest. You can get OK without them.

    → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +7 Vote: I do not like it

    Yes, only one letter will be split across sides and others will be used whole on one side only. You can use subset sum to check if sum X is possible or not.

    Solution:http://codeforces.net/contest/1070/submission/44593642

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Why have you assumed that any alphabet other than the one that will be split will either be completely in the smaller set or will not be there

      → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    Yeah, the same solution with bitset. code

    → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

where can i see test data?

→ Reply
»
6 years ago, # |
  Vote: I like it +37 Vote: I do not like it

L is very cool, thanks

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    How to solve it?

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +34 Vote: I do not like it

      Let's come up with a way to find answer if it is at most 2 and then we will show that it always find the answer.

      We want to distribute vertices in two classes, it is the same as giving each vertex 0 or 1. Let's say that vertex v gets xv (which is 0 or 1). Now I state that all our properties about parity of degree can be written as linear equations in . Suppose that vertex v initially had even degree. Then it is not important what is xv: in all cases v should have even number of neighbors with 1, in other words 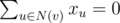. Now suppose vertex v initially had odd degree. Then if xv = 0 then v will have odd number of neighbors with 1, and if xv = 1 then v will have even number of neighbors with 1, in other words .

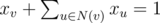      If this system of linear equations has a solution then we are done. How can it be that there is no solutions? Some equations contradict each other. In the only way is to add some of equations and get 0 = 1. Suppose that happens. Let's denote set of vertices corresponding to those equations C. C has odd number of vertices with initially odd degree (otherwise we would have 0 in the right side). Since we have 0 in the left side it is true that all xu have even coefficients, it is true also for vertices in C. That means that if we will look at subgraph induced by C all initially even vertices will have even degree and all initially odd vertices will have odd degree (don't forget that for odd vertices we add not only its neighbors but also itself). But we have odd number of vertices with initially odd degree, so sum of degrees of all vertices in this induced subgraph is odd which is impossible.

      Therefore there is always a solution with at most 2 components. Checking is there is a solution with 1 component is trivial, and for finding the solution we will use gaussian elimination with bitsets.

      → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +19 Vote: I do not like it

      Here is a different solution, that also shows we never need more than 2 states.

      completely useless alt-text

      44659832 — runs in O(N^3 / bitset)

      (the problem was discussed on some facebook group some time ago — apparently it also turned up on the POI)

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it +5 Vote: I do not like it

        Looks like it could be done without bitsets. I've implemented this idea and got AC with time complexity O(N^2 + sum(deg[i]^2)) which is not worse than O(N * M).

        → Reply
»
6 years ago, # |
  Vote: I like it +8 Vote: I do not like it

In L how to prove that answer is no more than 2? I guessed it and successfully got Accepted.

→ Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Can A be solved by DFS? I tried to solve it with memory search.But I could not pass it.

→ Reply
»
6 years ago, # |
  Vote: I like it +1 Vote: I do not like it

How to solve I ?

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 38   Vote: I like it +30 Vote: I do not like it

    It's not better to color two edges which are not adjacent.

    Consider the degree of one vertex, call it r. If r>2k, there is no solution. If r<=k, we can just ignore it. If k<r<=2k, we need to make at least r-k pairs of it's adjacent edges the same color, that is, 2(r-k) edges.

    So we need to choose 2(r-k) adjacent edges for each vertex, and each edge can be chosen at most once. This is a match problem (vertex matches edge). I used dinic to solve it.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +4 Vote: I do not like it

      Thank you very much. I have got it via your explanation.

      → Reply
»
6 years ago, # |
  Vote: I like it +4 Vote: I do not like it

Will there be an editorial put up?

→ Reply
»
6 years ago, # |
  Vote: I like it +21 Vote: I do not like it

Can E (Getting Deals Done) be solved using Ternary search?

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    It can (44592241), but binary is enough.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +3 Vote: I do not like it

      can you explain how it can be done with binary search?

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        F(d) = {0,1} — can we do all of the tasks that is less or equal to d. The values of this function will be in form of 1111100000. With binary search we should find 1-0 point, and result will be either in the last point with value 1 or in the first point with value 0.

        → Reply
        • »
          »
          »
          »
          »
          6 years ago, # ^ |
          ← Rev. 2   Vote: I like it 0 Vote: I do not like it

          So far, I've understood that one can binary search without the constraint of extra time after m tasks. However, how can you prove that the tasks will still be of the form 11..00.. even after adding this additional constraint?

          → Reply
          • »
            »
            »
            »
            »
            »
            6 years ago, # ^ |
            ← Rev. 3   Vote: I like it +6 Vote: I do not like it

            Actually, this constraint only doubles duration of each task except last group. Consider adding a single task Q, which is greater or equal then others.

            Let's suppose the place of new task is somewhere in the middle. Then time will grow by 2Q and some old task P will move to the last group and time will be decreased by P ≤ Q, so total grow is 2Q - P ≥ Q > 0. If last group is full, new group will be created for task P, and the time grow will be 2Q + prevLastGroup - P. If the new task will be inserted in the last group, total grow is Q.

            Total time increasing in any way and this is enough condition for described binary search to work. Another question is why this two points gives you an answer to the initial question.

            Let's suppose you reach the first overflow, so some tasks in the tail was dropped for the first time. Then we will add a new task at some place. Lets prove then at least one other task will be dropped. The new task is Q, the previous dropped is S ≤ Q, the new last task is P ≤ Q.

            If the last group is not full, then free space is less than S. If the last group is full, then there is a gap between last group and moment T. The size of this gap strictly less then prevLastGroup + S. If we add new task to the end of the sequence, it will be dropped. If we add new task to the middle, time will increase by 2Q + prevLastGroup - P which is strictly greater than the max gap size (prevLastGroup + S - 1).

            Feel free to correct me if I am wrong somewhere.

            → Reply
»
6 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

My output for the sample test case 1 of E (Getting Deals Done):

3 5

4 6

2 9

0 101

Why this is wrong? It is given that we can print any value of d.

→ Reply
»
6 years ago, # |
  Vote: I like it +6 Vote: I do not like it

How to solve C ?

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 4   Vote: I like it 0 Vote: I do not like it

    You can solve it greedy. The main observation is: you able to sort available tariffs by price in non-decreasing order and choose some of them greedy every day starting by cheapest and stopping when you got enough cores. Then just model tariff starts and finishes in historical order, accumulating paid amount per day. You also will need some data structure to keep active tariffs and their cost day-to-day, segment tree or Fenwick tree, and binary search to determine count of tariffs to buy today in log(m).

    See my submission 44600156 for implementation based on segment tree; its complexity is O(m * log2(m)).

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +3 Vote: I do not like it

      Binary search is not needed, Fenwick tree supports the operation "first index with prefix sum greater than x", 44588175

      → Reply
    • »
      »
      »
      5 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I can't understand your solution. Can you please explain more?

      → Reply
»
6 years ago, # |
  Vote: I like it +8 Vote: I do not like it

Will there be an editorial?

→ Reply
»
6 years ago, # |
  Vote: I like it +16 Vote: I do not like it

Can I get the editorial?

→ Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

How to solve problems G, I?

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    For G, you can try every possible position, call it x. Now you can greedily try to move the closest hero that can beat all monsters in the path to x, and if at the end you can move everyone, then you have found the answer. The complexity is O(N^3).

    → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to solve I?? QAQ

→ Reply
»
6 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

About problem B If the input data is

7
+0.0.0.13
+0.0.0.12/32
-0.0.0.2/31
-0.0.0.7/32
-0.0.0.10
-0.0.0.9/32
-0.0.0.8/31

output data is:

2
0.0.0.0/29
0.0.0.8/30

but my answer is:

2
0.0.0.2/29
0.0.0.10/32

I think my answer is also right,but it is WrongAnswer why?

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +15 Vote: I do not like it

    From the statement: "It is required that 32 - x rightmost (least significant) bits of subnet a.b.c.d/x are zeroes." 0.0.0.2/29 violates this requirement.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      Could you give an example?I do not understand.And why does 0.0.0.2/29 violate this requirement?

      → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I already understand it.Thanks.

      → Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

how to solve C ?? looks like some have done sweepline ..

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    That's not sweepline, you just consider a tariff task as two events, and do some proper segment tree over prices.

    → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to resolve H? I see it is a blute force problem. But I get timeout. Can someone give me a guide how to implement a blute force solution with any special skills?

→ Reply