Is it possible to perform such operations with array in quasilinear total time (precalculations and queries)? 1. add a number x on a segment [l;r] 2. count the number of all elements in [l;r] which are <x If it is possible to solve this problem offline, then a new question arises: is it possible to solve it online with amortized O(log(n)^k) time per query (where k is a constant)?
I know that if a number is added to only one element (pos), then the problem can be solved in O(log(n)^2) time per query online using a segment tree with a treap in each node which consists of the elements of the segment which corresponds to the node. I also know that the given problem can be solved in O(sqrt(n)*log(n)) time per query (again, this works online) using sqrt-decomposition (we divide our array into sqrt(n) blocks of the size of sqrt(n), and then we maintain for each block it sorted and a modifier which is added to all the block's elements). But here the query time is too long.











That sqrt approach is actually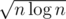 .
.
And for real tasks that’s much faster than all those overloaded polylogs.
I don't know even how to do it in O(sqrt(n log n)) per query. I can do it in O(sqrt(n)*log(n)): We split our array into blocks of size about sqrt(n) blocks, then we sort each block and add a modifier (initially 0). When we get a query of adding a constant, we do it element-wise in the blocks where l and r are, and in all the middle blocks we can just increase the modifier by the constant; and we should also rebuild the sorted versions of the blocks with l and r. Thus it takes O(sqrt(n)) for modifying and O(sqrt(n)log(sqrt n))=O(sqrt(n)*log(n)) for rebuilding, totally O(sqrt(n)*log(n)). When we get a query like 'how many elements in [l;r] are <k, we count them element-wise in the blocks where l and r are (in O(sqrt(n))) and for each of the middle blocks (O(sqrt(n)) times) we do binary search (in O(log(sqrt n))=O(log(n))) in its sorted version to find out how many elements in it are <k-modifier. Thus this type of query also takes O(sqrt(n)*log(n)).
And in my implementation it works for several seconds when n and q are about 2e5, not good.
Let block size be A. One can see that in fact the operation that leads to rebuild is “increase a range inside the block by x”. That means that your block can be divided into three parts — prefix and suffix (each of them might be empty) that remain untouched by that last update and a range somewhere in between. In other words, these can be represented as three sorted vectors that you have to merge (easy to do it in linear time).
Choose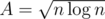 and here you go.
and here you go.
Edit number something: wrong, sorry.
Merge sort tree is updatable in O(logn)?
Edit number something: wrong, sorry.