As you know that Educational Codeforces Round 54 (Rated for Div. 2) was held yesterday. Perhaps, you solved 1076B - Divisor Subtraction without any difficulty. Now, I am thinking how to solve this problem if there are no less than 10^5 queries. Please, mention the complexity with approach.
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
15:39:11
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
15:39:11
Зарегистрироваться »
*есть доп. регистрация
→ Трансляции
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 23.11.2024 01:55:50 (i1).
Десктопная версия, переключиться на мобильную.
При поддержке
owowow
Any idea? Then, share with me.
Yes
Share your idea, please.
if you lower the limit of n to 1e7 than you can have as many queries as you want, but i dont think 1e10 is gonna do well for more than 100 queries...
There are around 1e4 primes lesser than 1e5 so you can optimize it to work for around 1e4 queries (and maybe faster with pollard rho?)
That is impossible to do so in time limit of 2 or 3 seconds, isn't it?
A simple 1e8 loop runs under 1 second easily in codeforces.
Has there any way to find at least a divisor of n smaller than sqrt(n) within at most 1000 loops where n<=10^10?
Isn't this question equivalent to integer factorization at the worst case? Then, I suppose there are no known way to do the task in 1000 loops...
I thaught that also...whatever,thanks bro....
As tfg mentioned above, for a lot of queries, to precompute all the primes in range [2, 1e5] would be fastest. Then your task must cost at most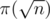
which is larger than 1000