Открытое личное первенство УрФУ 2012

12 лет назад, # |

I решается жадно. На каждом шаге пробуем посмотреть очередной фильм. Тогда складываем в вектор все уже посмотренные фильмы, сортируем его по времени и жадно смотрим.

→ Ответить

12 лет назад, # ^ |

Жадно смотрим — можно подробнее?

→ Ответить

12 лет назад, # ^ |

← Rev. 2 →

+13

для каждого студента поддерживаем время, когда он закончит смотреть какой-то фильм — end_i и предыщую красоту фильма c_i, для очередного фильма пытаемя из всех свободных студентов выбрать студента с максимальным c_i, но меньшим, чем красота текущего фильма.

→ Ответить

KirillB

12 лет назад, # ^ |

← Rev. 3 →

Я вроде такое и писал, только у меня WA3. Так и не понял в чем подвох.
upd. кажется понял, неверно выбирал

→ Ответить

Monyura

12 лет назад, # ^ |

А почему не студента с максимальным временем окончания фильма? Для вашего алгоритма, как я его понял, есть простой тест:
4 2
1 2 3
3 4 1
5 6 4
2 3 4
Пусть 1й студент посмотрит 1й фильм, а 2й студент 2й фильм. Тогда для 3 фильма мы выберем 1го студента, т.к. красота его фильма больше чем у 2-го, и для 4-го фильма уже не сможем выбрать никого. Или я что-то не так понял?

→ Ответить

12 лет назад, # ^ |

+10

сортируем его по времени и жадно смотрим.

ключевое слово — сортируем, так этот алгоритм валится тестом еще проще
100 200 5
1 2 4
300 400 3

→ Ответить

12 лет назад, # ^ |

+10

А куда именно жадно смотрим? Я ниасилил придумать жадность в этом месте, и решил с помощью наименьшего покрытия графа путями %)

→ Ответить

12 лет назад, # ^ |

+10

Авторское именно такое — покрытие графа путями. Но на контесте в УрФУ все сдавали жадину.

→ Ответить

Perlik

12 лет назад, # ^ |

← Rev. 2 →

А как именно? я делал двудольный граф. Ребро из i-ой вершины левой в j-ую правой если можно посмотреть фильм j после i-ого. Находим паросочетание максимальное, строим новый граф неориентированный, в котором есть ребро (i,j) если (i,j) или (j,i) есть в паросочетании. Далее помечаем все компоненты связности в этом графе пока есть студенты.
Еще пробовал искать по очереди паросочетания минимального веса мощностью 1,2,.. n, и лучшее выбирать.

→ Ответить

12 лет назад, # ^ |

А можно узнать суть 19 теста?

→ Ответить

Perlik

12 лет назад, # ^ |

У меня почему-то такое ВА27 получало упорно.

→ Ответить

12 лет назад, # ^ |

У меня тоже :( Из-за этого зафейлил контест. Так бы выиграл.

→ Ответить

gojira

12 лет назад, # ^ |

+39

Мне бы так контесты фейлить :)

→ Ответить

Fefer_Ivan

12 лет назад, # ^ |

+10

Я решал I другим способом.

Предположим, что у каждого фильма есть вес и нам надо найти ответ наибольшего веса. Тогда если i-тому фильму присвоить вес 2^{n - i - 1}, то мы сведем исходную задачу к этой.

Как решать задачу с взвешенными фильмами. Построим взвешенную сеть, где у каждого ребра пропускная способность равна 1. Каждому фильму поставим в соответствие две вершины: входную и выходную. Между входной и выходной вершинами одного фильма проведем ребро веса, равного весу фильма. Между выходной вершиной фильма i проведем ребра веса 0 ко входным вершинам всех фильмов, которые можно посмотреть после просмотра фильма i. Так же из истока добавим ребра веса 0 во все входные вершины, а из всех выходных — в сток.

Пропустим k единиц потока. Каждая единица потока — это один студент.

Так как 2⁹⁹ — это много, то пришлось писать на Java с BigInteger. Прошло с первой попытки.

→ Ответить

12 лет назад, # ^ |

← Rev. 2 →

пичаль((( у меня абсолютно то же самое не прошло(

→ Ответить

12 лет назад, # |

Как решать F? OEIS подсказал только 21 число:(

→ Ответить

12 лет назад, # ^ |

← Rev. 2 →

Критерий того, что набор (A₁, A₂, ..., A_n) с A₁ ≤ A₂ ≤ ... A_n подходит это A₁ + ... + A_k ≥ 3k(k - 1) / 2 для 1 ≤ k ≤ n, причем при k = n должно достигатся равенство. Необходимость очевидна, так как любые k команд разыгрывают между собой ровно 3k(k - 1) / 2 голов. В достаточность я поверил, и после того как увидел, что ее уже сдали, без сомнения закодил ДП, которое теперь уже без труда угадывается, но из-за дурацкого ML — 64MB пришлось сдать массив ответов в коде.

UPD. Исправил ≤ на ≥

→ Ответить

12 лет назад, # ^ |

При n = 3 возможен результат (0, 4, 5). Это не вписывается в предложенную схему, так как 0 + 4 > 3. То же самое с (1, 3, 5). Тут 1 > 0. Что я понимаю неверно?

→ Ответить

12 лет назад, # ^ |

должно быть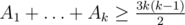 $\text{[math]}$

→ Ответить

12 лет назад, # ^ |

Есть идеи, почему этого достаточно?

→ Ответить

12 лет назад, # ^ |

← Rev. 2 →

+13

Если коротко, то можно свести задачу проверки возможности данной таблицы результатов к поиску полного паросочетания в двудольном графе, а потом применить теорему Холла. Унылое доказательство в первой правке :)

→ Ответить

it4.kp

12 лет назад, # ^ |

Еще OEIS говорит:

FORMULA Nonnegative integer points (p_1, p_2, ..., p_n) in polytope p_0=p_{n+1}=0, 2p_i -(p_{i+1}+p_{i-1}) <= 3, p_i >= 0, i=1, ..., n.

по этому условию можно написать динамику

→ Ответить

12 лет назад, # |

+10

Как решать E и H?

→ Ответить

12 лет назад, # ^ |

← Rev. 3 →

Можно получить такое решение H. Если дискриминант меньше нуля, ответ 1. Иначе ответ:
sqrt(1 + 3 * b^2 / a^2 — 12 * c / a), округленный вверх. Е — самому интересно)

→ Ответить

Madiyar

12 лет назад, # ^ |

еще можно бинпоиск)

→ Ответить

12 лет назад, # ^ |

А откуда бинпоиск?

→ Ответить

Madiyar

12 лет назад, # ^ |

перебираем ответ задачи код

→ Ответить

12 лет назад, # ^ |

Тоже писал бинпоиском, но во время контеста не сдал изза тупой ошибки с приведением типов: ф-ия проверки дискриминанта:

static bool d(int A, int B, int C, long n)
        {
                BigInteger _b = A * n * (n - 1) + B * (n);
                BigInteger _a = A * (n);
                BigInteger _c = A * n * (n - 1) * (2 * n - 1) / 6 + B * n * (n - 1) / 2 + (n) * C;

                BigInteger res = _b * _b - 4 * _a * _c;

                return res < 0;
        }

А надо было:

static bool d(BigInteger A, BigInteger B, BigInteger C, long n)
        {
            checked
            {
                BigInteger _b = A * n * (n - 1) + B * (n);
                BigInteger _a = A * (n);
                BigInteger _c = A * n * (n - 1) * (2 * n - 1) / 6 + B * n * (n - 1) / 2 + (n) * C;

                BigInteger res = _b * _b - 4 * _a * _c;

                return res < 0;
            }
        }

→ Ответить

12 лет назад, # ^ |

А как такая формула получилась?

→ Ответить

12 лет назад, # ^ |

Составляем уравнение a * x^2 + b * x + c + ... + a * (x + k — 1) ^ 2 + b * (x + k — 1) + c = 0. Если у него нет корней, то дискриминант меньше 0. Из этого составляется квадратное неравенство на k. Получится (k — 1)^2 + 2 * (k — 1) + 12 * c / a — 3 * b^2 / a^2 > 0. Получим два случая — или ответ 1 (подставляя вместо k, получим условие на дискриминант), или ответ — больший корень уравнения, округленный вверх (это сама формула).

→ Ответить

12 лет назад, # ^ |

+11

Сначала сворачиваем сумму f(x) + f(x + 1) + ... + f(x + k - 1). Получаем

$\text{[math]}$

Это квадратное уравнение на x. Так что считаем дискриминант. Он чудесным образом окаывается очень простым:

a² + 3b² - 12ac - a²k².

Откуда уже все и получаем. Не знаю как все делали, но у меня, чтобы не писать длинку, были какие-то извращения со знаковым и беззнаковым 64-битным целым типом.

→ Ответить

12 лет назад, # ^ |

А можно считать в даблах — для того, чтобы сравнить число с нулем, точности хватает.

→ Ответить

Sklyack

12 лет назад, # ^ |

А корень тоже как-то в целых числах вычисляли?
У меня зашло в даблах, но я не понимаю почему, ведь под корнем число порядка 10^18, а в мантиссе дабла всего 15 десятичных знаков (16-й как повезет), и кажется, что при преобразовании unsigned long long в double имеет место большая погрешность.

→ Ответить

dalex

12 лет назад, # ^ |

Я обычно корень вот так вычисляю:

ll sqrt(ll x) {
    ll s = (ll)sqrt(x + 0.0);
    while (s*s <= x) s++;
    while (s*s > x) s--;
    return s;
}

Вроде бы это не несет за собой проблем. Может красные подскажут, если проблемы все же есть.

→ Ответить

12 лет назад, # ^ |

У меня в E решение короче, чем в любой из остальных задач :)
Там ответ всегда да, причём номер кинозала для уранца с X руками можно найти только по числам n2, n3, n5, где X = 2^n2 * 3^n3 * 5^n5 * Y, (gcd(Y,30)=1).

→ Ответить

12 лет назад, # ^ |

-10

а можно поподробней?

→ Ответить

12 лет назад, # ^ |

Не хочется раскрывать всю задачу. То есть код выглядит так:

for i=1 to n
    read x
    n2 = 0
    for(; x % 2 == 0; x /= 2) n2++;
    // Аналогично n3, n5
    if(g==2) print f2(n2)
    if(g==3) print f3(n2,n3)
    if(g==4) print f4(n2,n3)
    if(g==5) print f5(n2,n3,n5)

Функции f2,f3,f4,f5 занимают не более 10-15 символов каждая. Например, f2(n2) = n2 % 2 + 1. Остальные могу раскрыть, если кому-то сильно надо. Но, мне кажется, интересней самому их найти.

→ Ответить

12 лет назад, # |

Как долго займет процесс добавления задач в основной архив?

→ Ответить

12 лет назад, # ^ |

Добавили

→ Ответить

12 лет назад, # |

+10

Ну и ради интереса: как решать C кроме рандом шафла?

→ Ответить

12 лет назад, # ^ |

Перебор показывает, что для n=5 всегда можно выиграть. Поэтому просто перебираем все перестановки суффикса длины min(n,5), а префикс не трогаем (за первые max(n-5,0) шагов он съестся поэтому мы работаем только с суффиксом)

→ Ответить

http://pastebin.com/a0uDPHcj

12 лет назад, # ^ |

← Rev. 2 →

-10

Зделал так как Вы написали, но ВА12 не знаю в чем может быть проблема.. может ктото может помочь? вот код:

UPD: Туплю должго быть: var basic = new[] { arr[arr.Length - 5], arr[arr.Length - 4], arr[arr.Length - 3], arr[arr.Length - 2], arr[arr.Length - 1] }; вместо: var basic = new[] { arr[arr.Length - 1], arr[arr.Length - 2], arr[arr.Length - 3], arr[arr.Length - 4], arr[arr.Length - 5] };

→ Ответить

12 лет назад, # ^ |

Если у нас есть хотя бы 5 карт, то всегда можем выиграть. Теперь если карт много, то N-5 положим в том же порядке, что у противника, а остальные 5 — переберем все перестановки. Если карт меньше 5 — тоже втупую переберем все перестановки, но в этом случае мы можем и проиграть.

→ Ответить

12 лет назад, # |

Как решать B? Пробовал переводить координаты в I координатную четверть, домножать их на 1000, брать по модулю 1000, потом искать точку, в которую отобразилось наибольшее количество установок, среди всех таких выбирать наиболее близкую к началу координат — WA 32.

→ Ответить

12 лет назад, # ^ |

Близость до начала координат меряется как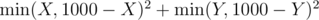 $\text{[math]}$ . То есть иногда ближе переехать в точку с отрицательной координатой. Возможно в этом ошибка.

→ Ответить

12 лет назад, # ^ |

Это я тоже учёл. Вот код: http://pastebin.com/1YGxjeSU

→ Ответить

12 лет назад, # ^ |

+12

Может проблема в точности? (int)(a * 1000) не всегда дает верный ответ.

→ Ответить

12 лет назад, # ^ |

А как тогда делать?

→ Ответить

12 лет назад, # ^ |

Перед приведением к инту прибавлять чуть-чуть, если положительно, отнимать чуть-чуть, если отрицательно. Или как-нибудь хитро сразу читать целочисленно.

→ Ответить

12 лет назад, # ^ |

Добавить EPS в случае когда a ≥ 0 и вычесть его в противном случае

→ Ответить

12 лет назад, # ^ |

← Rev. 4 →

Например, для чисел с тремя знаками после запятой можно (int)(a * 1000 + 0.5), если a неотрицательно, и (int)(a * 1000 — 0.5), если отрицательно.

→ Ответить

12 лет назад, # ^ |

Да, действительно, проблема была в этом. Спасибо!

→ Ответить

12 лет назад, # |

А как предполагалось решать J? Я сдал все полностью в целых числах, используя некоторые дикие хаки с НОДом, чтоб избежать переполнения long long. В принципе, если б не ошибка в ДНК :), мог бы даже с плюса сдать.

→ Ответить

12 лет назад, # ^ |

Аккуратное моделирование в даблах заходит

→ Ответить

12 лет назад, # ^ |

Навсегда теперь запомню, как может отрезок пересекаться с треугольником.

→ Ответить

12 лет назад, # |

+13

Интересно, как работал чекер задачи С? Если простой эмуляцией игры, то возникает вопрос — могло ли быть так, что игра зацикливается или длится очень долго? Ну и вообще интересная задача — насколько долго игра может затянуться в принципе...

→ Ответить

BekzhanKassenov

12 лет назад, # |

Я конечно тупой, но как решать А?

→ Ответить

12 лет назад, # ^ |

Например хешами.

А по-другому можно?

→ Ответить

12 лет назад, # ^ |

можно поддерживать баланс каждой буквы в дереве отрезков, и каждый раз смотреть если минимум и максимум балансов равен = 0, то ans++

→ Ответить

12 лет назад, # ^ |

Необязательно дерево отрезков, можно просто в каждый момент времени смотреть у скольки букв из алфавита количество совпадает с нужным.

→ Ответить

12 лет назад, # ^ |

а как это быстро находить?

→ Ответить

12 лет назад, # ^ |

Для первого отрезка посчитаем втупую, потом пересчитываем за O(1).

void inc(int ch, int d) // d = 1 для входящих в окно, -1 для выходящих
{
	if(cnt[ch] == needCnt[ch])
		sameCnt--;
	cnt[ch] += d;
	if(cnt[ch] == needCnt[ch])
		sameCnt++;
}

→ Ответить

12 лет назад, # ^ |

зачем! давайте заведем дерево отрезков!

→ Ответить