I am stuck on this following problem:
Given two strings of size n and m (1<=n,m<=100000), find the number of common substrings between this strings.
It will be really helpful if you can give me a solution.
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 156 |
| 7 | adamant | 151 |
| 7 | djm03178 | 151 |
| 7 | luogu_official | 151 |
| 10 | awoo | 146 |
I am stuck on this following problem:
Given two strings of size n and m (1<=n,m<=100000), find the number of common substrings between this strings.
It will be really helpful if you can give me a solution.
| Name |
|---|



It requires data structure that is called suffix array — array, which contains a permutation of numbers from 1 to n, where n is the length of a string. Number i in this array represents i-th suffix of a string, and suffixes are sorted lexicographicaly.
There is a nice way to build it in n log ^ 2 (there is also exists a way to build it in n log n, which is also quite easy (look here https://cp-algorithms.com/string/suffix-array.html), and even in O(n) (but algorithm in O(n) has relatively high constant factor, so it is not very practical).
So, lets build suffix array in O(n log ^ 2 n)!
Lets count polynomial hashes of a string (if you are not really familiar with polynomial hashes of a string, look here: https://cp-algorithms.com/string/string-hashing.html). So now we can check, whether two substrings of our string are equal in O(1) time!
Lets notice that we can compare lexicographicaly two suffixes in O(log n) time — lets use binary search and find longest common prefix of two suffixes. We can do it in O(log n) time. And then we can just compare the first letter that differs in those two suffixes, and we are done! So, we can just run std::sort on the permutation of numbers from 1 to n using this comporator and so we will get a suffix array of a string in O(n log n) (sorting) * O (log n) (each comparison works in O(log n))).
To solve our original problem let`s build the suffix array and count lcp[i] — longest common prefix of neigboring suffixes in the suffix array. (We can calculate lcp in O(n log n) using that binary search with hashing) (it is also possible to do this in O(n), which is describes in the article above). Than, lets sum the lcp values substruct this value from (n ^ 2 + n) / 2 and we are done! It is exactly the number of different substrings of a strings. For some proof look here: https://cp-algorithms.com/string/suffix-array.html#toc-tgt-10
Actually, I know how to find the number of different substrings in a string. But my problem is not that. I want to know "how many common substrings are there between two different strings"
Oh, sorry. I somehow misread the problem.
Well, let`s build suffix arrays of both strings, s and t. (array for string s#t where '#' in neither in s, neither in t and smaller than any other symbol).
It is a common knowledge is that every substring is a prefix of some suffix. Let`s iterate over the suffix of the string s which we choose. Fot or this string, we can find out longest prefix of the suffix that also occurs in t — simply look at the nearest left position in merged suffix array which belongs to string t and nearest right position in the merged suffix array which belongs to string t(via some simple dp for instance). So, now we know for each suffix of s longest prefix of it that belongs to t. So now we can iterate over suffix array and add max(longest_t[i] — lcp[i], 0) for ecach suffix of s to the answer (lcp[i] — lcp of i and i — 1 suffix in this case. (idea is similar to the one in my first comment).
It seems you know all to solve your problem. Let A — set of different strings of a (first given string). Let B — set of different strings of b (second given string).
Then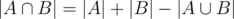 . You know how to calculate |A| and |B|, and you want to find
. You know how to calculate |A| and |B|, and you want to find  . Think a bit, how to obtain
. Think a bit, how to obtain 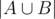 .
.
Let c = a + # + b. Then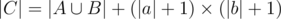 . Assuming, that character # is neutral element, which can't appear in strings.
. Assuming, that character # is neutral element, which can't appear in strings.
(|a| + 1) × (|b| + 1) — the number of substrings in c, that contain our neutral character #.