Блог пользователя oversolver

Efficient solution to add / sum problem
Автор oversolver, история, 6 лет назад, По-английски

We have n points (xi, yi). Let both x and y be different and from [1, n].

Initially, all points have zero value.

Two types of queries:

1) add X — adding +1 to all points with xi ≤ X

2) sum Y — calculate sum of values of points with yi ≤ Y

What is best known solution? (Problem not from running contest).

  • Проголосовать: нравится
  • +49
  • Проголосовать: не нравится

»
6 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

With square Root Decomposition we can have updates and queries in .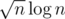

→ Ответить
»
6 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

You can do sqrt decomposition on either queries or divide in sqrt blocks by y-value, and in each block keep sorted by x value. Both solutions lead to sqrt*log complexity, but since you've asked for best known solution, I think you've already tried these.

→ Ответить
»
6 лет назад, # |
← Rev. 6   Проголосовать: нравится +11 Проголосовать: не нравится

Sort by Y, divide into K blocks, precalc number of points <= X for each block. For each block keep sum of all the points in this block, so updates will be processed in O(K). Queries for sum of complete block will give also O(K), and to process incomplete block you can store just one global Fenwick tree by X, so total time for sum query will be .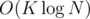

That gives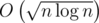 per query with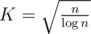

If you will add sqrt decomposition on queries instead of Fenwick, you will get per query.

→ Ответить
»
6 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

Is it an amazing coincidence that a similar problem shows up in the contest today. Take a look at 1093E - Intersection of Permutations.

→ Ответить