TL;DR This article features Modular class which can be conviniently used for modular arithmetic more "naturally".
Motivation
Recent round featured an interesting problem 1081C - Colorful Bricks (if you plan to solve it, read this later). Combinatoric solution requires you to calculate:
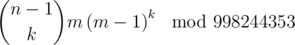
Many contestants failed pretest because of missing modulo operation somewhere in code.
Solution
Many contestants use functions like add(ll a, ll b) or mul(ll a , ll b) which makes implementation somewhat clumsy.
I present you an alternate approach using Modular class.
template <int MOD=998'244'353>
struct Modular {
int value;
static const int MOD_value = MOD;
Modular(long long v = 0) { value = v % MOD; if (value < 0) value += MOD;}
Modular(long long a, long long b) : value(0){ *this += a; *this /= b;}
Modular& operator+=(Modular const& b) {value += b.value; if (value >= MOD) value -= MOD; return *this;}
Modular& operator-=(Modular const& b) {value -= b.value; if (value < 0) value += MOD;return *this;}
Modular& operator*=(Modular const& b) {value = (long long)value * b.value % MOD;return *this;}
friend Modular mexp(Modular a, long long e) {
Modular res = 1; while (e) { if (e&1) res *= a; a *= a; e >>= 1; }
return res;
}
friend Modular inverse(Modular a) { return mexp(a, MOD - 2); }
Modular& operator/=(Modular const& b) { return *this *= inverse(b); }
friend Modular operator+(Modular a, Modular const b) { return a += b; }
friend Modular operator-(Modular a, Modular const b) { return a -= b; }
friend Modular operator-(Modular const a) { return 0 - a; }
friend Modular operator*(Modular a, Modular const b) { return a *= b; }
friend Modular operator/(Modular a, Modular const b) { return a /= b; }
friend std::ostream& operator<<(std::ostream& os, Modular const& a) {return os << a.value;}
friend bool operator==(Modular const& a, Modular const& b) {return a.value == b.value;}
friend bool operator!=(Modular const& a, Modular const& b) {return a.value != b.value;}
};
Using this code can be written more naturally in modular field just like integers. This implementation simplifies usage, for example:
// Chained Multiplication or Successive Simple Multiplication
Modular<998244353> a=1, m=123456789;
a *= m * m * m; // a = 519994069
// Inverse
a=inverse(m) // a=25170271
// fractions
Modular<> frac=(1,2); // frac=1*2^(-1) % 998244353 = 499122177
// Modular exponentiation
Modular<> power(2);
power=mexp(power,500); // power = 616118644
Credits to Jakube and here's the link to original source. Link: Modular.h











I have seen similar implementations before, but I'm not sure if performance is not an issue. Do you have benchmarks comparing this to the non-wrapped implementation, in terms of both time and memory usage?
I think having this in a critical loop (which runs, say 10^8 times) might be problematic, but I'm not sure; C++ compilers can do a lot of magic.
that's c++. such abstractions do not cost anything here.
Isn't there overhead for the function call? Or can we be certain it is inlined
you are right, overhead for function calls is possible but for such trivial function I just assume they are inlined (I use such class for several years, didn't have any problem).
I use a similar class. In my experience the abstraction doesn't noticeably reduce efficiency compared to manually applying the same operations, but it can cause you to use more operations that you actually need. In particular, when taking the sum of N numbers, it is more efficient to first sum them in long long, then reduce that sum, than to reduce after every addition.
Exactly what Wave said.
Perfomance in many cases of modular tasks is an issue and you should avoid copying by
const Modular&rather using plainconst Modular(since it doesn't really matter whether you put const here or not, you can keep it if you want compliler to help you a little) in most of your operators.See this: this. Although being too unrealistic, you should generally avoid passing references to classes where
sizeof(class)is around a single pointer due to a perfomance overhead over plain copy of that class.P.S. I don't see this
struct Modular <int N>as a good solution because such class makes it significantly harder to pass ints to functionsP.P.S. and yeah, specialization for
long longmodulo would've been really cool, since this is something really lame to implement over and overSince all the methods and friend functions are implemented in the class, they will be inlined by default, and there is no difference in passing argument by reference or by value.
being inline and being inlined is more or less orthogonal
integer do not form field btw
Your implementation is very limiting. First, only
intmodulo is supported, nolong longor any custom big integer class. Second, it won't work if the modulo isn't fixed, i.e. given in the input file.I have similar class that can be found for example in these submissions: 26577783 24552744. Indeed, it's very convenient and I never faced any performance issues.
Another issue is that it relies on the modulo being prime (the inverse is found using fermat's).
yes, this works for prime modulo which is very common otherwise you can replace
inversewith extended euclid.Because it is not very common where you need to find inverse in non-prime modulo (not for problems focused on extended euclid), so focusing on speed fermat is used.
btw you may use std::integral_constant when modulo is constant instead of creating new class manually
1 . Considering general modulo (1e9+7, 9998244353),
long longis not supported as multiplication function will change to somewhat like code below, which will not be efficient in case of common integer mod.2 . Submission (26577783) is not visible to me. Can you share code via other methods?
3 .
BigIntegersclasses typically contain modulo operation.Sorry, here's another submission 24552744
There's also efficient
long longmultiplication in there.Here's the result of running the code below in Custom test on Codeforces:
The results (2e8 iterations) are: