Если единственная единица стоит на пересечении r-ой строки и c-го столбца (в 1-индексации), то ответ: |3 - r| + |3 - c|.
Если k > n, решения нет. Иначе отсортируем квадраты по убыванию размеров. Теперь нам подходит любая точка, которая принадлежит k-ому квадрату, и не принадлежит k + 1-ому. Например, можно вывести координаты (ak, 0).
Первым делом проверим, что каждое число встречается во входных данных 4 раза. Если это не так, то решения точно нет. Иначе попытаемся восстановить круг. Так как циклический сдвиг не имеет значения, пусть 1 будет первым числом. Второе и третье число должны быть соединены с 1 и между собой, поэтому вариантов мало, их все можно перебрать. Зная эти 3 первых числа, оставшаяся часть круга однозначно восстанавливается за линейное время. Возьмем последние 2 числа из круга, далее найдем число, которое соединено с ними, но еще не входит в ответ, и добавим его в конец. Если такое число нашлось, то продолжим процесс. Если в результате получилось добавить все числа в круг, то это и есть ответ.
Рассмотрим такой простой путь v1, v2, ..., vr, что его нельзя продолжить добавлением вершины в конец, к vr. Это значит, что все соседи vr уже содержатся в пути. Найдем первую вершину в пути (vl), которая соединена с vr. Понятно, что vl, vl + 1, ..., vr — цикл, и он содержит всех соседей vr. По условию задачи, каждая вершина имеет хотя бы k соседей. Значит длина цикла не менее k + 1 ( + 1 получается за счет самой вершины vr).
Разделим ромб на 4 прямоугольных треугольника, как показано на рисунке ниже. В результате получится 1 треугольник размера k, 2 — размера k - 1, 1 — размера k - 2.
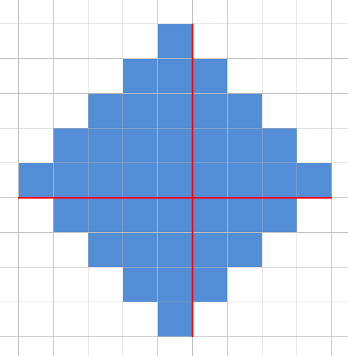
Разобьем задачу на 4 подзадачи. Самый удобный способ сделать это — 4 раза повернуть исходный массив на 90 градусов, и каждый раз запускать одну и ту же функцию, которая решает для одного треугольника. Функция будет возвращать 2-мерный массив, каждая ячейка которого будет содержать ответ для треугольника с вершиной в этой ячейке. Несложно понять, как совместить 4 таких массива, чтобы получить ответ для исходного ромба.
Основная идея решения для треугольника в том, что, зная ответ для одной клетки, мы можем "подвинуть" треугольник на единицу в любую сторону (вправо, вниз, влево или вверх) и пересчитать ответ за константное время. Вообще говоря, важны только 2 направления: вправо и вниз. А ответ для верхней левой клетки можно посчитать за O(k2) двумя вложенными циклами.
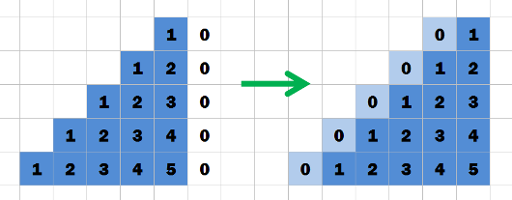
Определим следующие 5 функций:
Сумма на диагональном отрезке из k элементов:
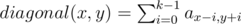
Сумма на вертикальном отрезке из k элементов:
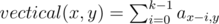
Взвешенная сумма на вертикальном отрезке из k элементов:
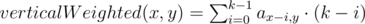
Сумма на треугольнике:
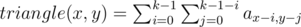
Взвешенная сумма на треугольнике:
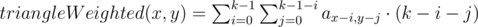
Посчитать первые 3 функции за O(nm) в сумме совсем просто. Остальные функции можно быстро считать так:
triangle(x, y + 1) = triangle(x, y) - diagonal(x, y - k + 1) + vertical(x, y + 1)
triangleWeighted(x, y + 1) = triangleWeighted(x, y) - triangle(x, y) + verticalWeighted(x, y + 1)
Формулы для перемещения треугольника в другие стороны почти ничем не отличаются.
You also need to mention that, for 263C - Circle of Numbers, how: - N=5 is trivial (any combination works) - N=6 there are 12/(6C2=)15 possible pairs, so ensure that the missing 3 pairs are not neighbours - N>6 probably your approach will work (N>=10 would be safest)
and also, please clarify what you mean by
..., there are only few possibilities. So let's try them all...For example, for N=1, say i discover that 1 is neighbours to 6 and 3, and 6 and 3 are neighbours to each other, it could be '1 (either 3 or 6) (either 3 or 6) ...' or '(either 3 or 6) 1 (either 3 or 6)...' What are you trying to say? maybe illustrate with a link to a AC submission, please.much appreciated.
Let's consider the number of the common neighbours of 1 and 3(say,t1) and the number of the common neighbours of 1 and 6(say,t2).
If t1=2 and t2=1, then it should be 1 3 6.
If t1=1 and t2=2, then it should be 1 6 3.
If t1=2 and t2=2, then it should be 3 1 6.
[deleted]
+1 for the tutorial! I hope that all next contests will have a similar one! And nice contest by the way :)
My solution to problem C is quite different from the tutorial:
Triangle means: for an edge(u, v), there exists k that both edge(u, k) && edge(k, v) exist.
Special cases should be noted: the given graph may not be connected!
I don't get it, why N = 6 is special case, can someone point it out please?
Actually I make use of this property: If N >= 7, then for three consecutive vertices (a, b, c), a will be connected with (d, e) and c will be connected with (f, g), and (d, e, f, g) will be distinct vertices. For N == 6, this property does not hold.
Thank you.
No problem :)
For N>=7, nodes X and Y are next to each other in the circle iff their adjacency lists look like this:
X(A,B,Y,E1) Y(A,B,X,E2)
where E1 != E2.
for special case, if each point is exactly connected to 4 other points and there're 2*n nodes, the whole graph must be connected
Do you mean 2n edges? Consider this case: put two valid n=5 cases together to get an n=10 case, this graph is disconnected but all nodes is connected with 4 other nodes.
It was really unfair not to rejudge problem D as many clearly wrong solutions passed(see this thread) and thus decreased the point of the problem. My solution may fail too in rejudge but fair result should be ensured.
take vertex = 1 + ( n * m + ( n ^ m ) + ( n & m ) + ( n | m ) ) % n; find max distance to all its neighbour, get accepted what is logic to solve it?
Does anybody have an idea for the problem E ?
В E с данными ограничениями достаточно было вначале посчитать частичные суммы на диагоналях, и для каждой клетки как для центра ромба считать за константное время сумму на клетках каждого уровня ромба, а потом домножать эту сумму на нужный коэффициент. Вот пруф, что операций будет мало: http://www.wolframalpha.com/input/?i=Maximum[k*%281000-2k%29*%281000-2k%29].
I have wrote a solution in Chinese, anyone can view it. here is my blog
Here is my approach for case N = 6 in problem C:
Because each node connects to exactly 4 others, there're always 3 pairs of nodes which are not neighbors. Find these 3 pairs and put them into the circle. Place node a of pair (a, b) in any position i from 1 to 3 (make sure it's still available), then place node b in position i + 3.
Я решал Е немного иначе. Я поворачивал матрицу на 45 градусов и искал сумму на квадратах, а не на треугольниках.
Я прочитал разбор D трижды, но ничего не понял. Можно подробнее, что там происходит?
I wonder why I got TLE in Div1.C by not checking if all numbers are repeated 4 times... It doesn't change the order, does it?
can someone please explain me that why we use |3-x| + |3 — y| in beautiful matrix
The problem asks to move the only '1' to the center of the matrix, which is located as (3, 3). For any position with (x, y), we need |x-3| + |y-3| steps to move it to the center. You may refer to Manhattan Distance for more details, and if you still have questions, welcome to discuss.
i am getting tle my code is for beautiful matrix question``
include include using namespace std;
int main() { int arr [5][5]; int x,y =0; for (int i = 1; i <=5; i++) { for (int j = 1; j <= 5; j++) { cin>>arr[i][j]; if (arr[i][j]== 1) { x =i ; y =j ;
} } } cout<<(abs(3-x)+abs(3-y)); return 0; } please help me out
If you use arr[5][5], then both i and j should not exceed 4. In other words, when i=5 or j=5, it leads to out of bound. You may use arr[6][6] instead.
why be have to take arr[6][6] as when we have to define an array we define it by its size ie is 5x5
The index in general starts from 0, and thus for arr[5], we could only use arr[0], arr[1],...,arr[4]
if i run my code in code editor for test case 1 . it give me correct output .but when i submit this code .they give me output 7 .why and what is the wrong
include<bits/stdc++.h>
using namespace std; int main() { ios_base::sync_with_stdio(false); cin.tie(NULL); int arr[5][5]={0}; for(int i=0;i<5;i++) { for(int j=0;j<5;j++) { cin>>arr[i][j]; }
} if(arr[2][2]==1) { cout<<"0\n"; return 0; } int move=1; int x,y; for(int i=0;i<5;i++) { for(int j=0;j<5;j++) { if(arr[i][j]==1) { x=i; break; } else move++; } if(x==i) break; // cout<<endl; }// cout<<move<<endl;
int cnt=0; for(int i=move;i<13;i++) { cnt++; } cout<<cnt<<endl; return 0;}
A pretty neat trick for Problem A.