cuom1999's blog

A property of triangulation
By cuom1999, history, 6 years ago, In English

"In a triangulation of a regular n-gon, there always exists a diagonal that divides the polygon into 2 small polygons and the smaller one has at least 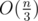vertices."

I saw this property in the NEERC 2014's editorial but still cannot prove it. Can anyone help me? Thank you!

  • Vote: I like it
  • +16
  • Vote: I do not like it

»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by cuom1999 (previous revision, new revision, compare).

→ Reply
»
6 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Take a dual tree to the triangulation (introduce a vertex inside every triangle and put an edge if faces share a diagonal) and find a centroid of this tree and diagonal you are looking for is one corresponding to the edge from centroid to its son with the biggest size of its subtree.

→ Reply
»
6 years ago, # |
  Vote: I like it +29 Vote: I do not like it

I think you mean NEERC 2015, not 2014.

Consider the triangle XYZ containing the circumcenter of the polygon. Without loss of generality let XY be the longest minor arc among XY, YZ and ZX. Then XY is the diagonal you're looking for, as it has at least n / 3 vertices on one side and at least n / 2 vertices on the other.

→ Reply