You are given a string of length 'n'.
If a string contains at least one character whose frequency is greater than or equal to the half of the length of the string, then the string is called superior.
You are required to find the length of the longest superior substring available in the given string.
Note: Here half is considered under integer division i.e. 5/2=2 , etc.
The string contains only lowercase English alphabets.
I have tried O(n^2) solution(s) with some optimization(s) which obviously got timed out. I realized that there are better:- O(nlogn) or O(n) approaches,can anybody explain them?
Link to the problem statement :- https://www.hackerearth.com/practice/algorithms/searching/binary-search/practice-problems/algorithm/superior-substring-dec-circuits-e51b3c27/
Thanks :-)











This should be solvable using a greedy solution using two pointer method. Take the largest substring from the left where there is a letter that makes it superior. As soon as this isn't true anymore, take another substring from the very next index and continue.
Deleted
Can you explain a bit more on how to actually proceed? Thanks!:)
Which part do you want me to elaborate?
Your solution is not correct. The function of the length of the superior substring is not monotonic. For example: aabcdeaa , in this string there is a superior substring of length 8 but not of length 6.
Whoops, thanks! Do you have any ideas?
For every alphabet, you can find the length of the largest substring in which it contributes as a dominant character. That can be done by building a prefix sum over that alphabet and for every index P[i] find a j < i such that P[i] — P[j] > (j — i) / 2. For more details, you can refer to the editorial.
Can't we perform binary search to check if we're able to achieve a superior string of given length, in O(n), for range low = 1, high = length of string.
No
Solution for "abcda" is 5 but no superior substring of length 4 exist.
If half was defined as actual half then there is a nice way to solve it. Remember there was a blog about something close to this a while back but now I can't seem to find it. Will use python notation to explain my idea.
Let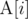 be defined as
be defined as
sum(1 for c in S[:i] if c=='a')which is the number of 'a' in the string at indices < i. For a substring S[a:b], a < b, to contain half or more 'a's then
which is the same as
This inequality basically solves everything, just go through all indices sorted by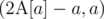 while keeping track of the smallest index you've seen and you're basically done. Here is some pseudo-code:
while keeping track of the smallest index you've seen and you're basically done. Here is some pseudo-code:
with this you can also do other fun stuff like calculating number of longest superior substrings and so on. The running time should be alphabet size times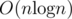 . It is possible to remove the
. It is possible to remove the 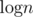 using bucket sort, and it might also be possible to remove the scaling with the alphabet size by some modifications to the algorithm.
using bucket sort, and it might also be possible to remove the scaling with the alphabet size by some modifications to the algorithm.
Iterate over a letter that will be most frequent, and change the string into a sequence where every occurrence of the chosen letter is
+1, and every other letter is-1. Then you're looking for the longest substring with a positive sum of values. This can be solved in O(n), so the whole problem is solvable in O(n·26).Nice Idea, but a minor change is required This problem becomes a little different because of integer division definition. Lets say the string is: abc. Focusing on 'a' we get , 1 -1 -1 and the longest subarray with positive/0 sum is of length-2(0-1) but actually, the answer to this case is '3' cuz 3/2=1 which is the frequency of 'a' , so we have to find the longest subarray whose sum is >= -1 , thanks for the idea though :)
Ok, that's a strange rounding definition in the problem. I agree it should be >= -1 in this case.
I did what you mentioned but it got timed-out on exactly 1 test out of all the tests : D, any ideas on further optimizations?
And yea, on a side-note, today's stream was awesome, thanks for so much contribution ! :-)
Show us your code. Put it in "spoiler" tags or paste it to pastebin or ideone.
And I'm glad you liked the stream :)
****Spoiler*****
The solution which passes all the tests except one is here:- https://ideone.com/wvpXju
Also, I created an O(nlogn) solution for finding the longest subarray with sum>=-1 . I feel maybe the time limits are too tight?
Thanks :-)
You can find the longest the longest substring with sum >= -1 in O(N).
For this you can just keep a record of first time you had any prefix sum.
Then largest substring ending at the index i with sum >= -1 would be
i, if prefix[i] >= -1
i - (minimum index having sum (prefix[i]+1)) + 1, if prefix[i] < -1
As I said, that part can be solved in O(n). Values of prefix sums are from interval [ - n, n] only, so you can sort them in O(n).
One approach is to compute x[value] as the shortest prefix with a sum equal to value. Then you must go through the sequence again and for every prefix you want to know: if this prefix sum is A, what is the shortest prefix with sum A - 1 or smaller? You can know this by computing prefix minima on the array x[].