AakashHanda's blog

Invitation to CodeNation Hiring Contest 2019
By AakashHanda, history, 6 years ago, In English

Hi Everyone,

CodeNation, Bengaluru is conducting an online hiring test on 26th January, 2019 at 5:00 PM IST.

Register here: https://goo.gl/forms/7aopASH1dchGbjHE3 for the Online Test Shortlisted candidates will win a chance to interview with us for SDE and SDE Intern positions.

Eligibility Criteria:

  1. Indian nationals
  2. 2019/2020 graduates
  3. Students from all the branches of BTech, Mtech, Bsc, Msc, BCA, MCA, MS .
  4. Students who have never interviewed with CN or have interviewed before July 2018

Upd:

  1. Contest Link: Link
  2. Password: CN26119
  • Vote: I like it
  • +15
  • Vote: I do not like it

Comments Comments (19)
| Write comment?
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by AakashHanda (previous revision, new revision, compare).

→ Reply
»
6 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Where is the contest link??

→ Reply
»
6 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Auto comment: topic has been updated by AakashHanda (previous revision, new revision, compare).

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to solve mnDist? Optimized Floyd–Warshall?

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it -6 Vote: I do not like it

    yes, i solved it in O(20*60*30*60*30) => O(T*1/4*N^4). For T = 20 & N = 60, i guess it should pass.

    → Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it +3 Vote: I do not like it

How to solve MXSUM? Link to Problem Statement

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +11 Vote: I do not like it

    It can be solved by simply making 4 cases and calculating the maximum answer of the 4 cases:

    Let value(i) = |a[i] — a[i — 1]|

    We need to maximize (|a[r] — a[l — 1]| + |a[r + 1] — a[l]| — value(l) — value(r + 1)) ...(1)

    (1) can be written as:

    max(max(a[r] — a[l — 1], a[l — 1] — a[r]) + max(a[r + 1] — a[l], a[l] — a[r + 1]) — value(l) — value(r + 1))

    Now we have 4 possible options here,

    one of them is

    max(a[r] — a[l — 1] + a[r + 1] — a[l] — value(l) — value(r + 1)) = max(a[r] + a[r + 1] — value(r + 1) — a[l — 1] — a[l] — value(l))

    Now as its easy to see that r and l have been separated and we can calculate separately for l and r in O(n).

    Then we can iterate on r and maintain the best index or location for l.

    → Reply
»
6 years ago, # |
  Vote: I like it +8 Vote: I do not like it

A: Graph question about adding an edge to minimize cumulative sum of distances between each pair of nodes.

B: Reversing subarray of an array once to maximize "value" of array

C: Shortest path while visiting all nodes in set I before moving to set J.

D: Expected value problem

Solutions for any of these problems would be appreciated :)

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +6 Vote: I do not like it

    Expected value problem : Let the elements of array be A1, A2, ...An. I can't seem to prove this but answer is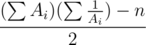 . This got accepted.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
      ← Rev. 5   Vote: I like it 0 Vote: I do not like it

      there are total of n! ways to take the order of removal of elements..and in each permutation, there will be exactly one term where ai is in denominator..if we observe the total sum from all permutations clearly..it can be seen that every aj (other than ai) will be present in numerator sum when ai is in denominator (remaining_sum/ai ) in n!/2 permutation(i.e for all permutations in which aj is after ai) ..

      i.e sum gotten when ai is in denominaotor from all perm. = (n!/2 * (sum of all elements — ai)) / ai

      using the above described idea by solving sum from all permutations/ n! we will get the above mentioned formula.. :)

      → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I didn't get a chance to read the questions. Could you please elaborate on what B was ?

    → Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 3   Vote: I like it +3 Vote: I do not like it

    someone pls ans..graph question. (q.1 : minimising sum of all pair shortest path by adding one edge)

    → Reply
»
6 years ago, # |
  Vote: I like it +6 Vote: I do not like it

Consider any two indices i and j. The only two possible sums they will be able to contribute are ai / aj and aj / ai. The first one will come in the final expression if index i is picked before j and the second one otherwise. Now, among all the n! permutations, in exactly half of them, i comes before j and vice-versa in the other half,

Thus, Expected Answer =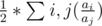

Upon reducing it a bit, you'll get the above formula.

→ Reply
»
6 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Can we get the editorials for the problems

→ Reply
»
6 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Anyone else facing the issue of not able to write code in the editor?

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I missed the test. Can we somehow see (and submit) problem statements now?

The contest link says Test is not active at this time

→ Reply