I am trying to find number of elements smaller than or equal to a particular value inside the multiset. I want a logn time approach. I have tried using distance(s.begin(),s.upper_bound(val)). But using distance method could take O(N) time in worst case.Can someone help me.
→ Pay attention
Before contest
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
5 days
Register now »
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
5 days
Register now »
*has extra registration
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Nov/25/2024 17:51:59 (j2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











You can't use multiset for that. Alternative data structures are segment trees and policy based data structures. see this
Fenwick tree too.
In C++, a.begin() can be subtracted from upper_bound(a.begin(),a.end(),x) to find the 0-based offset position of the first item in the sorted vector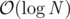 method may be applied to solve the Game of Two Stacks problem.
method may be applied to solve the Game of Two Stacks problem.
vector<T> athat is greater thanx. Note that if this position is equal to a.size(), then the largest value in the vector (i.e. a.back()) is less than or equal tox. ThisBut sadly, you can't do the same with sets(or Multiset).
Yes, because the iterator subtraction binary operator
-is undefined for both set and multiset data structures. Iterators of both containers are not random-access iterators. However, if this task is required for a larger number of queries, a simple way to apply the iterator-difference method is to copy the sorted set or multiset to a vector like that.and what do you think is the complexity of copying n elements from set to vector ?
The function call push_back may do memory reallocation, which can raise the complexity to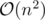 . However, if the required vector size is allocated before the copying operation, then random-access should be constant-time and the complexity should remain as
. However, if the required vector size is allocated before the copying operation, then random-access should be constant-time and the complexity should remain as 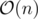 . Traversing a multi-set implemented using binary tree should be done in
. Traversing a multi-set implemented using binary tree should be done in 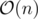 , check Tree Traverasls. Therefore, the complexity of the entire copying task should be
, check Tree Traverasls. Therefore, the complexity of the entire copying task should be 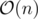 . It would be helpful to run a small program to confirm or refute this hypothesis.
. It would be helpful to run a small program to confirm or refute this hypothesis.
UPDATE: The following experimental results confirm roughly the linear-time complexity of copying the multiset to sorted vector.
Experiment
The following is a suggested C++14 solution based on the AVL balanced binary tree presented in Geeksforgeeks. Note that keys in the balanced binary tree should have distinct values. A multiset is implemented by counting the number of times the same key is inserted.
https://ideone.com/Fdupoh
UPDATE: A performance comparison between
AVL::multiset<int>andstd::multiset<int>was performed using 2,000,000 randomly generated integer keys. A new functionwas introduced to the container
AVL::multiset<T>. Similar to the standard library function std::copy, the introduced function copies all the sorted keys from the AVL multiset to the container starting from the forward output iterator positionresult, and considering the case when the same key was inserted two or more times. If the input parameterdistinctis passed astrue, any key is copied only one time even if it was inserted two ore more times. The results of the performance comparison shown in the program output of the previous link demonstrate that the introduced function callb1.copy_all(a1.begin())is 21 times faster than copying all the keys in thestd::multiset<int> b2object using the standardfor(auto b:b2)loop. Furthermore, the results show that inserting the 2,000,000 randomly generated integer keys tob1is about 3.21 times faster than inserting the same keys tob2.