Разбор Educational Codeforces Round 59

№	Пользователь	Рейтинг
1	tourist	3993
2	jiangly	3743
3	orzdevinwang	3707
4	Radewoosh	3627
5	jqdai0815	3620
6	Benq	3564
7	Kevin114514	3443
8	ksun48	3434
9	Rewinding	3397
10	Um_nik	3396

№	Пользователь	Вклад
1	cry	167
2	Um_nik	163
3	maomao90	162
3	atcoder_official	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	156
8	TheScrasse	154
9	Dominater069	153
9	nor	153

1107A - Разбиение последовательности цифр

Разбор

Решение (Vovuh)

#include <bits/stdc++.h>

using namespace std;

int main() {
#ifdef _DEBUG
	freopen("input.txt", "r", stdin);
//	freopen("output.txt", "w", stdout);
#endif
	
	int q;
	cin >> q;
	for (int i = 0; i < q; ++i) {
		int n;
		string s;
		cin >> n >> s;
		if (n == 2 && s[0] >= s[1]) {
			cout << "NO" << endl;
		} else {
			cout << "YES" << endl << 2 << endl << s[0] << " " << s.substr(1) << endl;
		}
	}
	
	return 0;
}

1107B - Цифровой корень

Разбор

Решение (Ne0n25)

#include <bits/stdc++.h>

using namespace std;

int main() {
	int n;
	cin >> n;
	for (int i = 0; i < n; i++) {
		long long k, x;
		cin >> k >> x;
		cout << (k - 1) * 9 + x << endl;
	}
}

1107C - Brutality

Разбор

Решение (Vovuh)

#include <bits/stdc++.h>

using namespace std;

int main() {
#ifdef _DEBUG
	freopen("input.txt", "r", stdin);
//	freopen("output.txt", "w", stdout);
#endif
	
	int n, k;
	cin >> n >> k;
	vector<int> a(n);
	for (int i = 0; i < n; ++i) {
		cin >> a[i];
	}
	string s;
	cin >> s;
	
	long long ans = 0;
	for (int i = 0; i < n; ++i) {
		int j = i;
		vector<int> vals;
		while (j < n && s[i] == s[j]) {
			vals.push_back(a[j]);
			++j;
		}
		sort(vals.rbegin(), vals.rend());
		ans += accumulate(vals.begin(), vals.begin() + min(k, int(vals.size())), 0ll);
		i = j - 1;
	}
	
	cout << ans << endl;
	
	return 0;
}

1107D - Сжатие

Разбор

Решение (Vovuh)

#include <bits/stdc++.h>

using namespace std;

const int N = 5200;

int n;
bool a[N][N];

void parse_char(int x, int y, char c) {
	int num = -1;
	if (isdigit(c)) {
		num = c - '0';
	} else {
		num = c - 'A' + 10;
	}
	for (int i = 0; i < 4; ++i) {
		a[x][y + 3 - i] = num & 1;
		num >>= 1;
	}
}

int main() {
#ifdef _DEBUG
	freopen("input.txt", "r", stdin);
//	freopen("output.txt", "w", stdout);
#endif
	
	
	scanf("%d", &n);
	char buf[N];
	for (int i = 0; i < n; ++i) {
		scanf("%s", buf);
		for (int j = 0; j < n / 4; ++j) {
			parse_char(i, j * 4, buf[j]);
		}
	}
	
	int g = n;
	
	for (int i = 0; i < n; ++i) {
		for (int j = 0; j < n; ++j) {
			int k = j;
			while (k < n && a[i][k] == a[i][j]) ++k;
			g = __gcd(g, k - j);
			j = k - 1;
		}
	}
	
	for (int j = 0; j < n; ++j) {
		for (int i = 0; i < n; ++i) {
			int k = i;
			while (k < n && a[k][j] == a[i][j]) ++k;
			g = __gcd(g, k - i);
			i = k - 1;
		}
	}
	
	cout << g << endl;
	
	return 0;
}

1107E - Вася и двоичная строка

Разбор

Решение (Roms)

#include <bits/stdc++.h>

using namespace std;

const int N = 102;
const long long INF = 1e12;

int n;
string s;
int a[N];

long long ans[N][N];
long long dp[2][N][N][N];

long long calcDp(int c, int l, int r, int cnt);

long long calcAns(int l, int r){
	if(l >= r) return 0;
	long long &res = ans[l][r];
	if(res != -1) return res;

	res = 0;
	for(int cnt = 1; cnt <= r - l; ++cnt){
		res = max(res, calcDp(0, l, r, cnt) + a[cnt - 1]);
		res = max(res, calcDp(1, l, r, cnt) + a[cnt - 1]);
	}

	return res;
}

long long calcDp(int c, int l, int r, int cnt){
	if(cnt == 0) return calcAns(l, r);
	long long &res = dp[c][l][r][cnt];
	if(res != -1) return res;
	
	res = -INF;

	for(int i = l; i < r; ++i){
		if(c == s[i] - '0')
			res = max(res, calcAns(l, i) + calcDp(c, i + 1, r, cnt - 1));
	}

	return res;
}

int main(){
	cin >> n >> s;
	for(int i = 0; i < n; ++i)
		cin >> a[i];

	
	memset(dp, -1, sizeof dp);
	memset(ans, -1, sizeof ans);

	cout << calcAns(0, n) << endl;	

	return 0;
}

1107F - Вася и бесконечные кредиты

Разбор

Решение (Roms)

#include <bits/stdc++.h>

using namespace std;

const int N = 505;
const long long INF = 1e18;

int n;
long long a[N][N];
int up[N], down[N], k[N];
long long u[N], v[N];
int p[N], way[N];

int main(){
	cin >> n;
	for(int i = 0; i < n; ++i)
		cin >> up[i] >> down[i] >> k[i];
	
	for(int i = 0; i < n; ++i)
		for(int j = 0; j < n; ++j)
			a[i + 1][j + 1] = -(up[j] - min(i, k[j]) * 1LL * down[j]);

	long long res = 0;
	for(int i = 1; i <= n; ++i){
		p[0] = i;
		int j0 = 0;
		vector<long long> minv (n + 1, INF);
		vector<char> used (n + 1, false);
		do{
			used[j0] = true;
			int i0 = p[j0],   j1;
			long long delta = INF;
			for (int j = 1; j <= n; ++j)
				if (!used[j]){
					long long cur = a[i0][j] - u[i0] - v[j];
					if (cur < minv[j])
						minv[j] = cur,  way[j] = j0;
					if (minv[j] < delta)
						delta = minv[j],  j1 = j;
				}
			for (int j = 0; j <= n; ++j)
				if (used[j])
					u[p[j]] += delta,  v[j] -= delta;
				else
					minv[j] -= delta;
			j0 = j1;
		}while (p[j0] != 0);
		do {
			int j1 = way[j0];
			p[j0] = p[j1];
			j0 = j1;
		} while (j0);

		res = max(res, v[0]);
	}

	cout << res << endl;
	return 0;
}

1107G - Вася и максимальный заработок

Разбор

Решение (Roms)

#include<bits/stdc++.h>

using namespace std;

const int N = int(3e5) + 99;

struct node{
	long long sum, ans, pref, suf;
	
	node () {}
	node(int x){
		sum = x;
		x = max(x, 0);
		pref = suf = ans = x;
	}
};

node merge(const node &a, const node &b){
	node res;
	res.sum = a.sum + b.sum;
	res.pref = max(a.pref, a.sum + b.pref);
	res.suf = max(b.suf, b.sum + a.suf);
	res.ans = max(max(a.ans, b.ans), a.suf + b.pref);
	return res;
}

int n, x;
pair<int, int> p[N];
node t[N * 4];

void upd(int v, int l, int r, int pos, int x){
	if(r - l == 1){
		assert(pos == l);
		t[v] = node(x);
		return;
	}
	
	int mid = (l + r) / 2;
	if(pos < mid) upd(v * 2 + 1, l, mid, pos, x);
	else upd(v * 2 + 2, mid, r, pos, x);
	
	t[v] = merge(t[v * 2 + 1], t[v * 2 + 2]);
}

node get(int v, int l, int r, int L, int R){
	if(L >= R) return node(0);
	
	if(l == L && r == R)
		return t[v];
	
	int mid = (l + r)/ 2;
	return merge(get(v * 2 + 1, l, mid, L, min(mid, R)),
				 get(v * 2 + 2, mid, r, max(L, mid), R));	
}

int main() {
	scanf("%d %d", &n, &x);
	for(int i = 0; i < n; ++i){
		scanf("%d %d", &p[i].first, &p[i].second);
		p[i].second = x - p[i].second;
	}
	
	sort(p, p + n);
	for(int i = 0; i < n; ++i) upd(0, 0, n, i, p[i].second);
	
	vector <pair<int, int> > v;
	for(int i = 1; i < n; ++i)
		v.emplace_back(p[i].first - p[i - 1].first, i);
	sort(v.begin(), v.end());
	
	long long res = 0;
	set <pair<int, int> > s;
	for(int i = 0; i < n; ++i){
		s.insert(make_pair(i, i + 1));
		res = max(res, 1LL * p[i].second);
	}
	
	int l = 0;
	while(l < v.size()){
		int r = l + 1;
		while(r < v.size() && v[l].first == v[r].first) ++r;
		long long d = v[l].first * 1LL * v[l].first;
		
		for(int i = l; i < r; ++i){
			int id = v[i].second;
			auto it = s.upper_bound(make_pair(id, -1));
			assert(it->first == id);
			assert(it != s.begin());
			auto R = *it;
			--it;
			auto L = *it;
			s.erase(L), s.erase(R);
			L.second = R.second;
			
			auto nd = get(0, 0, n, L.first, L.second);
			res = max(res, nd.ans - d);
			s.insert(L);
		}
		
		l = r;
	}
	
	cout << res << endl;
	return 0;
}

Комментарии (40)

Показать архивные | Написать комментарий?

zetoh

6 лет назад, # |

Someone help with the solution for problem-B. I can't "easily" get it :( How did it go from the formula to (k−1)⋅9+x

→ Ответить

raj1238

6 лет назад, # ^ |

← Rev. 2 →

Any number's one digit sum equivalence is equal to number modulo 9

Helpful Link:- https://math.stackexchange.com/questions/1789533/why-is-n-1-mod-91-equal-to-summing-all-digits-till-one-digit-is-left

LilyWhite

← Rev. 4 →

Assume you understand the given formula.

Then, you will easily find that S(x) repeats every 9 integers.

So, you can write it as my + n, y should be related to k, n should be related to x, m should be a constant.

The numbers 1 to 9 are the first cycle. Its digital roots are itself.

The numbers 10 to 18 are the second cycle.

Randomly pick two integers from the first and the second cycle, throw it into the my + n, you should then get the formula.

theanswer

Just write a small function to print all results from 1 to 100, you can easily see the cycle pattern exist there. hope this can help.

aps

+14

Problem G:
For every diff[i], I calculated the range in which it is maximum and took maximum suffix from left side and maximum prefix from the right side to calculate the answer.
Before constructing the segment tree,just to verify the logic I submitted the code with O(n) function to calculate max prefix and suffix expecting a TLE, but surprisingly it got ACed. Submission: 49068594
Are the test cases weak or is the time complexity of this solution lesser than O(n^2)
EDIT: neal answered it here

jef

For problem D, the brute force solution apparently runs fast enough.

gold1103

Yes,my brute force solution runs for 800+ ms.So I don't think this problem is very good and I don't know why this problem's difficulty is 1800. The time complexity just O(n²*c) ,c is the number of divisors of n

-9

c can be treated as a constant.

HCHC

I think c can't be treated as a constant...c changes when n changes...but certainly , c is always less than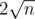 $\text{[math]}$ ......

Brijesh1in

On the one hand, if some segment of kind [1+lx , 1 + (l+1)x], where l is the value from the range [0;n/x−1], contains different digits then we cannot compress the given matrix.

Can someone explain me this with an example ??

c4big2

Please.. Someone explain me this with an example too.

AK18

for example:- let us assume that the size of given matrix A is 8 and we are using x = 2, then values of Ceil(8/2) = 4,Ceil(7/2) = 4 which means B[4][4] is equal to A[8][8], A[7][8], A[8][7],A[7][7]. which will not be possible if these values are different.

AnishG

Problem G: Solved it using segment trees(max segment tree) and lazy updates. Start iterating i from 1 to n. For a fixed i, a node j(<=i) will contain the answer for the segment j to i. So at each iteration, make a query from 1 to i. For the update part, when going from i to i+1, add (a — c[i+1]) to the range (1 to i) and maintain a stack to store the gap values for the range. For the stack update, if the new value i.e. (d[i+1] — d[i])^2 is smaller than the top value of stack, just add the negative value of it to the stack with it's range and also update it's value in the segment tree. If the new value if larger than the top value of stack, keep popping the top value(these values also need to be updated in the segment tree) until the new value is smaller than the stack's top value. Submission: 49103066

GreatWhite

-8

Why additional time is not given for Java programmers? Even the solution given in editorial for problem D is giving TLE in Java.

Riqirez

In task F we don't have to pick every credit, so shouldn't the formula be min(0, rest of formula)? Every Hungarian algorithm (that I found) assign all of n elements. Or just b[i]*k[i]<=a[i], but the statement doesn't include it?

NeonSkies

Regarding the tutorial for problem E.

I think it should be l ≤ mid ≤ r instead of 1 ≤ mid ≤ r here.

also mid<=r only if cnt=1

ansrespls

dp_{dig, l, r, cnt} = max{ans_{l, mid - 1} + dp_{dig, mid + 1, r, cnt - 1}}

what is the difference between these two?

dp_{dig, l, r, cnt} = max{ans_{l, mid - 1} + dp_{dig, mid, r, cnt}}

i mean is there something wrong with the second one?

sumit_kumar

Someone please explain the solution for problem-E, I didn't understand it from the tutorial.

pajenegod

Made a solution just doing recursion on strings to show the idea (solution). I think this is a bit easier to follow.

Xiao_Zhuang

Nice Approach, I tried this and got AC, but before that I had tried to recursively remove each block of consecutive digits(same 1s or Os). Algorithm is right but I got TLE, I don't understand why it is. Can you explain what happen? HERE IS MY CODE: https://codeforces.net/contest/1107/submission/49218582

The difficult part of this problem is not really to calculate the answer but to do it quickly. The reason why my code doesn't get TLE is that I practically only modify the beginning of the string, and if you think about it all the strings that is created will basically be a substring of the original string (except for the beginning part). So the number of strings I create are very limited.

In your code you are not doing it nearly as neatly because you are deleting parts of the string everywhere (not just in the beginning). So you will create a ton of different strings, probably exponentially many, and because of that get TLE.

Yeah I understand your code, that is your state either is substring of original string or combination of two substrings of original string. The number of different substring is nC2 ~ N^2 and the number of combination of 2 substrings is (N^2)C2 ~ N^4, so your complexity is O(N^4).

And my code may be up to N! So it gets TLE.

Thanks for your help!

To be technical, its not either a substring of the original or a combination of two substrings. It is always a string on the form '0...0' + S[a:b] or '1...1' + S[a:b] so there are n³ possible different strings.

Yep, sorry. So it runs in N^3 right?

The algorithm will ever only visit n³ strings but for each string it will do at most n² work. This is because for each string it might need to lookup n strings in a hashtable. So it runs in n⁵ with a very good constant, this could be lowered to n⁴ by playing around with indices instead of strings.

manojeet24

For Question B Digital root,We an use S(x)=x mod 9.

jakab922

I will give a proof in this comment on why the formula for 1107B - Digital root works.

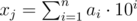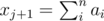To see that the formula is true you can prove that $\text{[math]}$ and $\text{[math]}$ gives the same value or it is invariant under the formula. In the case of x_j substracting 1 means that the trailing 0s become 9s so the disappear modulo 9 and if k is the first non-zero digit of x_j then its value will decrease by 1. Then we can do something like this:

$\text{[math]}$

It's not hard to see that given a b-ary number system where b is a positive integer if we define a similar process then the number x will end up in S_b(x) which can be characterized like:

The proof is the same as the above just replace 10 with b and 9 with b - 1.

Good

← Rev. 3 →

good

silversRayleigh

Can someone please explain the editorial of E in more detailed way ?

soul_voyage

Can someone explain why DP calculation in E is correct i.e. why there exist 'mid', why optimal solution for DP doesn't contain more than one segment which will lead to 'cnt' number of 'dig' instead of just a segment [mid, r]?

Upd: Got it.

Pj18

5 лет назад, # |

In D why can't we use binary search on divisors of n to find max value of x

vovuh In D why can't we use binary search across the divisors of n to find x?

vovuh

5 лет назад, # ^ |

Because the function isn't monotonic. For $$$n=12$$$ if the answer for $$$2$$$ and $$$4$$$ is true then it is not necessary that for $$$3$$$ the answer also will be true.

Example (uncompressed):

Test

010101010101
010101010101
010101010101
010101010101
010101010101
010101010101
010101010101
010101010101
010101010101
010101010101
010101010101
010101010101

Thanks

dnpshuser

A different approach for problem D here

Using gcd

BITree

interesting approach.

Whosoever solves problem E.

Please let me know how the complexity of the solution is O(n^4).

mehuld

4 года назад, # |

For Problem G: I used Kadane's algorithm but it gives wrong answer on test 7 and test 36 only. Could anyone point out the issue with this approach. Code with some comments.

Casio991ms

2 года назад, # |

-10

Simple bruteforce is enough for 1107D — Compression. https://codeforces.net/contest/1107/submission/160440328

Блог пользователя awoo