Let's look at a simpler problem. How many coins do you have to flip on average to get 2 Heads in a row?

For this we define E(n) being "expected number of flips if I already have n heads". Obviously E(2) = 0 and we just want E(0).

How do we compute E(0)? There is a 50% chance that we get tails, so that is still E(0) but  + 1 because we still flipped the coin. There is a 50% chance that we get heads, so that is E(1) and also  + 1 because we also flipped the coin. So that is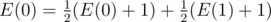 , and notice if you distribute the fractions everything becomes +1 in the end.

So to answer your question, yes you put the +1 for invalid prime AND for valid prime. But you put the +1 inside the parenthesis, and the gets multiplied and distributed. The +1 is outside the parenthesis.