I would like to invite you all to the International Coding Marathon 2019, under the banner of Technex'19, IIT (BHU) Varanasi.
Technex is the annual techno-management fest of Indian Institute of Technology (BHU), Varanasi organized from March 8 — 10, 2019.
International Coding Marathon is the flagship event of Byte The Bits, the set of programming events organized under Technex. ICM is brought to you by Mentor Graphics. It will take place on Friday, 8th March 2019, 21:00 IST. The contest will be held on Codechef.
The problemset has been prepared by hitman623, dhirajfx3, _shanky, drastogi21 and me (Enigma27). We would like to express our heartiest thanks to _hiccup and prakhar28 for their constant help in preparing the contest.

Prizes -
Overall 1st — INR 15,000
Overall 2nd — INR 10,000
India 1st — INR 9,000
India 2nd — INR 5,000
IIT(BHU) 1st — INR 6,000
IIT(BHU) 2nd — INR 4,000
IIT(BHU) Freshmen 1st — INR 1,000
Some of our previous contests :
ICM Technex 2017 and Codeforces Round #400 (Div. 1 + Div. 2, combined)
ICM Technex 2018 and Codeforces Round #463 (Div. 1 + Div. 2, combined)
Participants will have 2 hours 30 minutes to solve 7 problems. The scoring will be ICPC style.
Good luck everyone! Hope to see you on the leaderboard.
UPD — Contest begins in 1.5 hours
UPD1 — Contest begins in 15 minutes
UPD2 — Contest has ended. Congratulations to the winners. They will be contacted soon.
We deeply regret the inconvenience caused due to the problem ICM03. We will try to avoid such things in the future.
Editorials will be uploaded soon. Feel free to discuss the problems in the comment section.
UPD3 — The editorial is up.



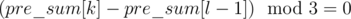
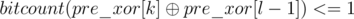
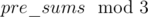 in a
in a 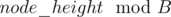 and then taking the index corresponding to the minimum value as
and then taking the index corresponding to the minimum value as 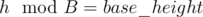 will be marked special. Hence there can be at most
will be marked special. Hence there can be at most 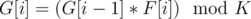
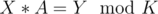 , for some
, for some 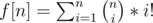 , where
, where 







Why isn't the contest organized on CF like in the last years?
Last year they faced some criticism on problem ideas(old ideas) and judging errors so they will now shift to Codechef where this happens on regular basis and so it will not be a surprise.
And you see.. contest has one problem removed and it's now unrated.
We want to distribute the prizes and we do not have enough problems for a CF div1+div2 Round. Also, we had less time to prepare the contest.
Anyways, I still hope that you will enjoy the contest.
Atlest you could have involved demoralizer,he would hve prepared the whole pset by himself.You all are noobs.
Well if he is that good, he could still do it all on his own. Then we can hold one on codeforces as well. I think two days must be more than enough time by his standard to do a div1+div2, as well as yours. We would really appreciate any help as per your capability, that is if you have any!
i m accepting i am a noob,but you are also a noob.and secondly if you are from iitbhu,why werent u included in psetting????bcz u r a noob.
Someone doing or not problem-setting is his own wish. What if i rejected because i wanted to participate in a contest my colleagues prepared. Besides, by your logic, i am pretty sure that your friend demoralizer wasn't invited, so he must be a noob. So why are you suggesting such a person who can hold a div1+div2 on his own. This suggest that you are not only a noob, but mentally damaged as well.
I don't know who he is and why he's saying all that...
Sorry brother, not anything against you. That was just reply for what he was asking.
Long challenge has still 4 more days left and this contest too is rated for all. What will happen if current div2/div1 contestants become div1/div2 after this contest while long still going on?
What usually happens is that rating changes of any short contest that happens during long challenge, come after long challenge rating changes.
Auto comment: topic has been updated by Enigma27 (previous revision, new revision, compare).
What was wrong in problem ICM03? I got Ac and suddenly it got removed.
There was some problem in the author's solution.
How can I know whether my solution was correct or not??
Most likely it is incorrect like author solution. Seems that this problem couldn't be solved for such big constraints. Maximal matching could be reduced to this problem in log iterations, and as I know there is no known algorithm for 10^5 edges
Is there any solution for this problem had the edges been smaller?
I dont know such solution
https://ideone.com/V4g0Jb .... that is my solution .... can you explain how it is wrong ???
Consider the following case:
5 4
1 2
2 3
3 4
4 5
1 2 3 4 5
Answer maybe both 17 or 18, depending upon which node you choose first as there are multiple choices for highest degree node.
thanks ...that was helpful ....
How to solve Pika-Pika?
It can be solved using persistent segment tree on Trees. We first make a frequency segment tree on all the numbers encountered from Root (say 1) to other nodes.
Then to deal with query (U, V), we can decompose the frequency of the elements lying on that path as Frequency till U + Frequency till V — 2 * Frequency till LCA + the value of LCA.
Then the query can simply be answered by descending the segment tree as: If sum of values on left <= X, then take all elements on left and go to right with (X — sum of elements on left), otherwise go to left.
Complexity: (N + Q) logN
Code: http://p.ip.fi/bo0f
Thanks! This is quite a good trick
It is equivalent to performing an implicit binary search over the maximum power of a pokemon that we can defeat. I solved it using an explicit binary search. Great idea though.
Is Pika-Pika about flattening the tree and then using Mo's algorithm / sqrt-decomposition along with binary indexed tree to calculate the required prefix sum using binary search? Is O(n * sqrt(n) * logn) accepted for these constraints?
I solved in O(n log^2) by parallel binary search
Did u apply parallelism on the flattened array? then how do u cover the vertices that are occuring exactly twice in that range.
I have many many questions.
Is there some easy solution for task with tree or just HLD wih O(log3) per query?
Also I can not understand why people adding constraints like n·m ≤ 105, did you think that current version is so nice and you need to make it a little bit ugly?
And what is solution for sequence problem it was most interesting to me at this contest (at least before I find out what is expected solution)?
Sequence problem is really cool :)
First, note that if some G[i] is equal to 0, this must be last element of sequence. So, lets number of non-empty sequence of numbers 1, 2, .., k-1 be ans(k) and answer to problem will be 2*ans(k) + 1 (because to every sequence we can add 0 to the end).
Now lets look on sequence h[i] = gcd(g[i], k). It is not hard to see, that h[i] is always divisible by h[i-1]. And h[i] can be only divisor of k.
So, let dp[i] be number of non-empty sequences of numbers 1, 2, .., k-1, which ends on such number x, such that gcd(x, k) = i. We are only interested in such i, that are divisors of k.
Let f[i] be number of non-empty sequences of numbers 1, 2, .., i. This values can be calculated with formula f[i] = i * (f[i-1] + 1). Note that f[i + mod] % mod = f[i] % mod, so we are only interested in first mod values of f, which can be easily precalculated in O(mod).
Now, how many there are numbers j, such that gcd(j, k) = i? It can be shown that this is phi(k / i). (As we are only interested in phi of divisors of k, it can be calculated quick enough).
So, now dp[i] = f[phi(k / i)] * (1 + S), where S denotes sum of dp[j], where j is divisor of i. And answer to the problem is sum overall dp[i].
Complexity is something like O(K^2/3 + mod).
Thanks for this long and clear explanation! Task looks really good.
I have only one question (part which was only problem to me during contest too). Why is f[i]=i*(f[i-1]+1)? I do not understand multiplication by i.
I believe it can be proven by induction but I hope there is some nice proof with combinatorics.
f[n] = n + n*(n-1)+n*(n-1)*(n-2)+...+n*..*1
Logic behind this formula is following — first we choose how many numbers we use is sequence (let k). On first place we can choose any number, on second — any but first, and so on. So there are n*(n-1)*...*(n-k+1) ways to choose group with k numbers.
Now, f[n] = n * (1 + (n-1) + (n-1)*(n-2)+...+(n-1)*..*1), which is equal to n*(f[n-1] + 1)
Thanks for explanation, now everything is perfect clear. I had first part of formula and than I didn't see recursive connection between n and n - 1.
I tried something like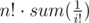 . And second thing was known to me from math classes, but not useful :D
. And second thing was known to me from math classes, but not useful :D
https://oeis.org/A007526 might be a good reference :)
Thanks for your explanation but only one question why f[i+mod]%mod = f[i]%mod ???
You can see that f[mod]=0 (has mod as factor), f[mod+1]=(mod+1)*(0+1)=1, and than continues in same manner
By induction we can prove: Suppose that f[i]%mod=f[i+mod]%mod.
Now f[i+1+mod]= (i +1 +mod)*(f[i+mod]+1)%mod= (i+1+mod)*(f[i]+1)%mod = (i+1)*(f[i]+1) % mod = f[i+1].
I have mathematical explanation for sequence problem though I figured it out very late into the contest.
Let d be the order of element x in Zk. Then, observe that order of G[i] always divides order of G[i-1](by Lagrange's Theorem: "Order of subgroup always divides order of group" and G[i] belongs to group generated using G[i-1] as generator) and in operation G[i] = (G[i - 1] × F[i])%K, order can decrease or remain equal. And also, observe that ord(G[i])<ord(G[i-1]), then x × G[i] = G[i - 1] will never hold. So, it will take care of the distinct property of G[i]. Now, we can do dp over the order of G[i] and use the fact that number of elements of order x is phi(K/x) since order of element a =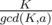 .
.
For the tree problem, we thought of 2 solutions, one using persistent segment trees and another using a square-root trick on tree. Details can be found in the editorial.
The constraint n * m < = 105 was not added after the problem was made. Also, we did not think that flipping the grid about diagonal would make it ugly. But, I agree that it could have been better.
The solution for the sequence problem can be found in the editorial soon.