Многомерные деревья

№	Пользователь	Рейтинг
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

№	Пользователь	Вклад
1	cry	167
2	maomao90	163
2	Um_nik	163
4	atcoder_official	161
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	nor	153
9	Dominater069	153

Всем привет. У меня появилось 2 вопроса, нагуглить которые эффективно я не смог, поэтому сюда напишу.
1. Может кто-нибудь дать ссылки на задачи на двумерное дерево отрезков?
2. Кто-нибудь может рассказать немного про квадродерево? Ну или хотя бы дать ссылки на толковые статьи, а то все, что я смог найти, так это описание в вики, да вот эта небольшая статейка. Суть я понял, но вот как именно строить все равно не очень понятно. Плюс нигде не могу найти внятной асимптотики. PavelKunyavskiy писал где-то, что работает за корень, на вики написано, что за log, а здесь вообще я не пойму, что значит "за O(N)".

Комментарии (9)

Написать комментарий?

NegaTeeF

12 лет назад, # |

На прошлой харьковской зимней школе были лекции про квадродерево. Можно попробовать там поискать в архиве

→ Ответить

Perlik

12 лет назад, # ^ |

Имеется ввиду 2012 года? 2011 и 2010 я просмотрел, вроде нет таких лекций. А 2012 года на сайте нет.

Burunduk1

+13

Понятия КД-дерево и Квадро-Дерево нужно различать.

То, что работает за $\text{[math]}$ , называется КД-деревом.

Возможно, имеется в виду моя лекция (Харьков-2012). Тогда текст можно найти здесь. Часть 4. Страница 5. Тема "КД-дерево". Видео лекции вроде гуглится...

В википедии сказано, что в среднем случае КД-дерево работает за $\text{[math]}$ , а в худшем за O(N^{1 - 1 / k}), где k — размерность пространства. Для k = 2 получаем ровно $\text{[math]}$ .

P.S. Здесь везде КД-дерево = структура данных, построенная от N точек. Если у нас есть таблица m × m, то N = m², соответственно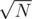 $\text{[math]}$ = m.

+11

Спасибо! Классная лекция, кстати.

Break-Neck

← Rev. 2 →

Извиняюсь, не то.

Programist

← Rev. 3 →

+12

Здесь есть задачи с харьковской зимней школы на двумерное дерево отрезков.

Здесь видео с прошлой харьковской зимней школы.

Его просто совсем недавно выложили.

indy256

O(N) в https://sites.google.com/site/indy256/algo/quad_tree означает временную сложность прямоугольного запроса count(x1, y1, x2, y2) на сетке NxN. Согласен, что написано непонятно.

Пример, на котором достигается N тут http://apps.topcoder.com/forums/?module=Message&messageID=1064330

Там рассматривается запрос в виде полоски шириной 1, который приводит к просмотру N клеток 1x1, например count(0, 0, N-1, 0).

Если я правильно понимаю, то хуже чем O(N) быть не может. А если мы заполним всю сетку NxN значениями, а запрос выполняется за O(N), то в этом случае вроде как получается, что запрос работает за корень.

За сколько оно работает зависит от конкретной задачи. За корень будет для множества точек на плоскости. (Правда видимо эта структура называется KD-дерево) По ссылке где непонятное "O(N)" насколько я понимаю речь идет про время работы за длину границы фигуры, на которой делается операция.

Блог пользователя Perlik