Hi. For the next problem I can not think of how to find a solution with graph searches (I thought it was backtraking but my college professor told me that I should use graph searches, which I do not know much about, to solve it).
As input we obtain a matrix (3x4) of connections ("|" or "-") which we must decode in the least amount of movements, to avoid that the bomb explodes. As an output inform one of the possible solutions.
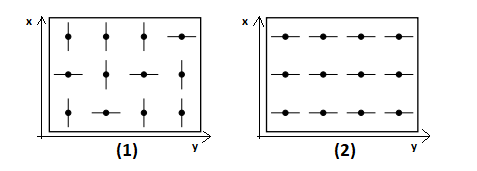
The decoding consite in that the matrix must contain only characters "-". To achieve this they tell us that if we move an element of the matrix, both the values of the column and row of the matrix change. For example if I move the element (0,0) of the matrix in this case the "-" change to "|" and vice versa in the column 0 and row 0. In the image (where (1) represents the input matrix and (2) the decoded matrix) a solution to inform would be:
(0,3), (2,1)
How to design an algorithm that solves this problem without using backtraking directly? Thank you in advance











As you are looking for the least amount of movements solution, just rearrange your backtrack to BFS-like algorithm. The vertices are board's "states" and the edge between two states is if we can do one move to achieve it. Of course it's pointless to compute whole graph, you can find edges if you are considering given vertex.