Bekh's blog

Question about memory reduction in Dynamic Programming problem
By Bekh, history, 5 years ago, In English

Hello,

I was trying to solve 383E - Vowels. Using the technique described here: https://codeforces.net/blog/entry/45223

I managed to get AC here: 61233188 using regular memory reduction (Reducing one of the dimensions to the size of 2).
I don't understand how it can be reduced to one-dimensional like this: 61233599.

Here is an image (with my amazing paint skills :P) to demonstrate my understanding of the dp dependencies in this problem: 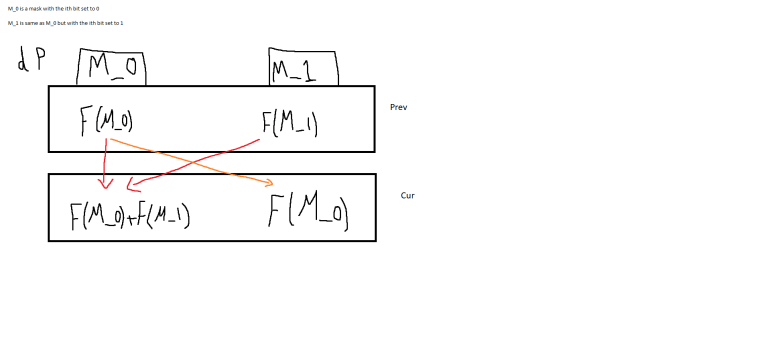Untitled.png

I can't see how these updates are done in the solution with only one dimension.

Any help would be appreciated.
Thanks.

  • Vote: I like it
  • +3
  • Vote: I do not like it

»
5 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Auto comment: topic has been updated by Bekh (previous revision, new revision, compare).

→ Reply
»
5 years ago, # |
  Vote: I like it +11 Vote: I do not like it

It's like with knapsack where you count ways to get some sum of weights.

for(int s = MAX; s >= 0; s--) if(s - weight >= 0) ways[s] += ways[s-weight]

If you iterate over indices in good order, you don't need an extra array. It's important that possible transitions go in only one direction (here from smaller to bigger indices).

Also, you shouldn't worry too much about memory like $$$N$$$ vs. $$$2 \cdot N$$$. It rarely matters.

→ Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    It's clear to me why this technique works for the problem you're mentioning. Here's my visualization for it: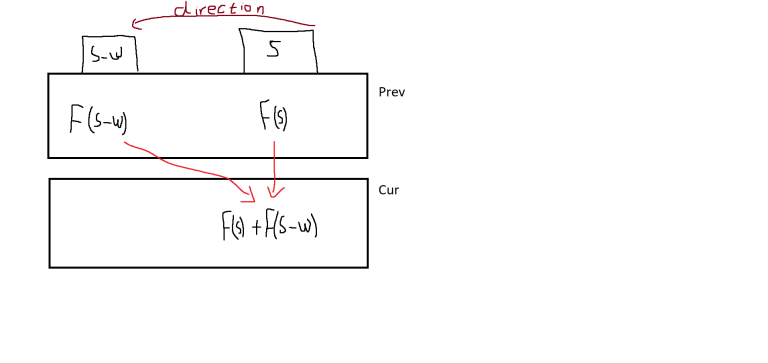 Untitleda7322d16e5b8db5f.png

    But it is still unclear for me how to apply the same technique for the problem above >,>

    → Reply
    • »
      »
      »
      5 years ago, # ^ |
        Vote: I like it +3 Vote: I do not like it

      Arrows in the bitmask problem are also only in one direction. Notice the if ((1<<i)&msk).

      → Reply
      • »
        »
        »
        »
        5 years ago, # ^ |
          Vote: I like it +3 Vote: I do not like it

        I still don't get how the transitions in the 2 codes are equivalent.

        When the $$$ith$$$ bit is $$$1$$$.
        In the first submission: it assigns the value of mem[prv][msk ^ (1<<i)] to mem[cur][msk]. We can't do in place updates here because mem[cur][msk ^ (1<<i)] would have been updated by a new value.
        In the second submission: it adds the value of mem[msk ^ (1<<i)] to $$$mem[msk]$$$.
        I don't get how the assignment in the first code is equivalent to the addition in the second code.

        Also when $$$ith$$$ bit is $$$0$$$.
        In first code it updates with mem[prv][msk] + mem[prv][msk ^ (1<<i)].
        In the second code, it does nothing.

        Here's how I visualize the transitions in the second code, which is obviously not equivalent to my visualizations of the first code (image in the blog):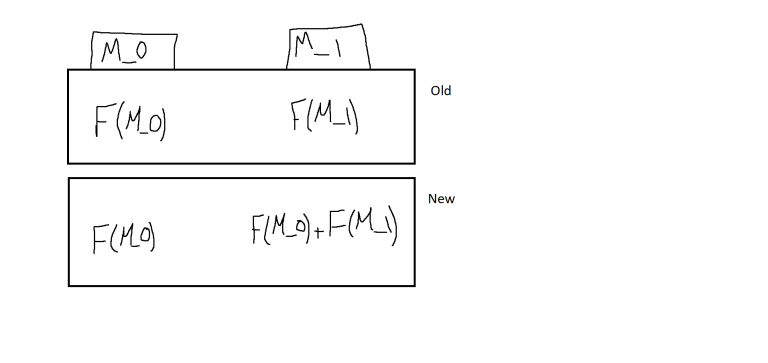 Untitled05efc0bfda445cd7.png

        What am I missing?

        → Reply
        • »
          »
          »
          »
          »
          5 years ago, # ^ |
          ← Rev. 2   Vote: I like it +3 Vote: I do not like it

          The first code swaps two values for some reason (e.g. at 01101 and 11101), that's strange and I don't think ever necessary in SOS problems.

          → Reply
          • »
            »
            »
            »
            »
            »
            5 years ago, # ^ |
            ← Rev. 3   Vote: I like it 0 Vote: I do not like it

            I was trying to compute for each $$$msk$$$:
            $$$F[msk] = Summation(A[x])$$$ for every msk&x == 0.

            So, if our current state is bit $$$i$$$ and mask $$$msk$$$.
            If current bit is $$$1$$$, the masks we're looking for must have this bit set to $$$0$$$, the answer will be mem[i + 1][msk ^ (1<<i)] (The swap you're talking about).
            If the current bit is zero, then this bit can be either zero or one, the answer will be mem[i + 1][msk] + mem[i + 1][msk ^ (1<<i)]

            → Reply