Блог пользователя chugaev

Размещение отрезков в контейнерах
Автор chugaev, 5 лет назад, По-русски

Столкнулся со следующей задачей.
Есть N отрезков, для каждого отрезка известны координаты начала и конца. Также имеется неограниченное количество контейнеров. Отрезки можно разместить в одном контейнере, если они не пересекаются, при этом двигать отрезки нельзя. Необходимо минимизировать количество контейнеров. Помогите найти оптимальный алгоритм решения.

Данные для задачи:

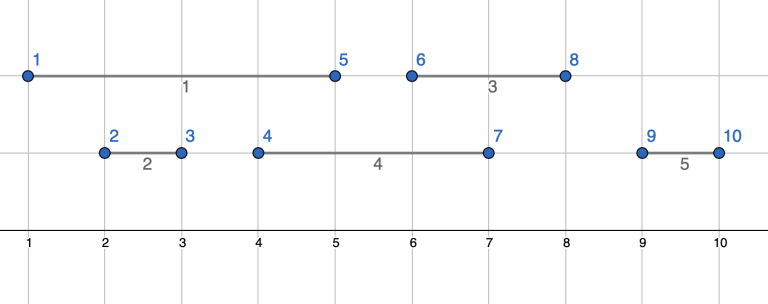
Первое число N — количество отрезков(1 <= N <= 1000), далее N пар чисел — координата начала и координата конца каждого отрезка. В качестве ответа — количество контейнеров и для каждого контейнера номера отрезков которые попали в этот контейнер. Пример:

Ввод:

5
1 5
2 3
6 8
4 7
9 10

Вывод:

2 - количество контейнеров
2 4 5 - номера отрезков в первом контейнере
1 3 - номера отрезков во втором контейнере

  • Проголосовать: нравится
  • 0
  • Проголосовать: не нравится

»
5 лет назад, # |
← Rev. 2   Проголосовать: нравится +17 Проголосовать: не нравится 
set<pair<pair<int, int>, int>> ranges; // сюда складываем отрезки, второй элемент пары - индекс во вводе, нужен для ответа
vector<vector<int>> ans; // здесь ответ - списки отрезков в котейнерах

while (!ranges.empty())
{
    auto it = ranges.begin(); // берём левый отрезок
    auto cur = *it; // сохраняем отдельно в пару
    ranges.erase(it); // и удаляем, т.к. он уже использован

    ans.push_back({cur.second}); // добавляем новый контейнер, пока что там только текущий отрезок

    while (true)
    {
        // Ищем самый левый непересекающийся с текущим отрезок
        auto nxt = ranges.lower_bound({{cur.first.second + 1, INT_MIN}, INT_MIN});

        if (nxt == ranges.end())
            break;

        // Добавляем в текущий контейнер и удаляем
        ans.back().push_back(nxt->second); 
        cur = *nxt;
        ranges.erase(nxt);
    }
}

$$$O(N \log N)$$$

→ Ответить
»
5 лет назад, # |
← Rev. 3   Проголосовать: нравится 0 Проголосовать: не нравится

Можно написать еще такое жадное решение: для решения необходимо поддерживать множество созданных контейнеров, отсортированное по самой правой границе отрезке, который в них находится. Тогда, если обрабатывать отрезки в порядке неубывания левой границы, контейнер, в который нужно положить текущий отрезок, можно искать бинарным поиском (если бинарный поиск не найдет подходящий контейнер, нужно добавит новый).

→ Ответить