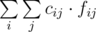hriss95's blog

Max-cost matching and flows
By hriss95, 12 years ago, In English

Hey guys, I've been trying to solve 1076 in Timus and I'm familiar it can be done with Hungarian algorithm or using flows, but can someone explain to me or give me a link(in English preferably) for Hungarian algorithm with O(n^3) complexity. And also, can someone tell me how to transform this problem to a flow problem. I would be very thankful if there is any response :)

  • Vote: I like it
  • 0
  • Vote: I do not like it

»
12 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

http://translate.google.com/translate?sl=auto&tl=en&js=n&prev=_t&hl=en&ie=UTF-8&eotf=1&u=http%3A%2F%2Fe-maxx.ru%2Falgo%2Fassignment_hungary (I think so !)

→ Reply
  • »
    »
    12 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Sometimes translation is very poor, for example, "Description of wood pieces in the base case". "wood" should be translated as "tree" :)

    → Reply
»
12 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

http://community.topcoder.com/tc?module=Static&d1=tutorials&d2=hungarianAlgorithm

connect Wi to source, Jj to the sink if you want to solve it using min cost max flow

→ Reply
  • »
    »
    12 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Can you explain which is Wi and which is Jj and what should be the flow and the cost of each edge. Thanks for the TopCoder link. I haven't noticed they have a tutorial about that :)

    → Reply
    • »
      »
      »
      12 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      given N workers (Wi) and M jobs (Jj), cij — cost of i-th worker to perform j-th job. Let's build a bipartite graph as described in this article and add source and sink.

      costs: cij for edges connecting Wi and Jj and 0 for the rest.

      max capacities: 1 for all edges.

      fij — flow on edge (i, j) provided by min cost max flow algorithm. It can be either 0 or 1; fij = 1 means i-th worker have to perform j-th job.

      Answer will be equal to

      → Reply