Задача А
Для получения максимального возможного результата нужно просто отсортировать слагаемые в порядке неубывания коэффициентов (коэффициенты учитываются со стоящими перед ними знаками + и -). Не нужно обращать внимание на a++ или ++a! Вопрос заключается в том, почему это правильно.
Во-первых, рассмотрим выражение, содержащее только a++. Тогда наше утверждение очевидно: выгодно умножать 'a' на маленькие коэффициенты, пока значение 'a' маленькое, и на большие коэффициенты, когда оно становится больше. То же самое происходит в случае трицательных значений коэффициентов или 'a'. Конечно, это не строгое доказательство. Я надеюсь, что вы еще подумаете над ним, если пока не поняли.
Во-вторых, рассмотрим выражение k*a+++k*++a, где k - некотрый коэффициент, одинаковый для обоих слагаемых. Пусть начальное значение 'a' равно a0. Вычисляя значение выражения обоими способами, получаем: k * a0 + k * (a0 + 2) = k * (a0 + 1) + k * (a0 + 1). Поэтому в данном случае порядок неважен.
В-третьих, пусть наше выражение k*a+++l*++a, где k и l - различные коэффициенты. Это выражение может принимать два разных значения k * a0 + l * (a0 + 2) и k * (a0 + 1) + l * (a0 + 1). Первое значение больше второго тогда и только тогда, когда k < l. Аналогично можно рассмотреть выражение k*a+++l*++a.
Таким образом, если имеются два последовательных слагаемых с одним и тем же коэффициентом, мы можем переставлять или не переставлять их. Если имеются два последовательных слагаемых с различными коэффициентами, мы должны поставить раньше то слагаемое, у которого коэффициент меньше. Применяя эти рассуждения, пока необходимо, получаем последовательность слагаемых отсортированных по коэффициентам.
Задача B
Эта задача решается жадно. Будем перебирать заданные числа последовательно, пока не встретим 1. Затем продолжим перебирать числа в поиске числа 2, потом 3, и т.д.
Задача С
Авторское решение работает за O(n2) по времени и требует O(n2) памяти. Также проходили решения за  времени и с O(n) памяти.
времени и с O(n) памяти.
 времени и с O(n) памяти.
времени и с O(n) памяти.Переформулируем задачу. Дано множество отрезков на прямой, и нужно найти максимальное его подмножество, такое, что отрезки в нем не пересекаются 'частично'. Два отрезка [a, b] и [c, d] пересекаются частично, если, например, a < c < b < d.
Возьмем все концы данных трезков, отсортируем их и посчитаем динамику: dl, r --- максимальный возможный размер подмножества, отрезки в котором не пересекаются частично и расположены между l-м и r-м концом (в отсортированном порядке) включительно. Мы хотим вычислять dl, r, имея уже посчитанные значения di, j для всех l ≤ i ≤ j ≤ r, но [i, j] ≠ [l, r]. Сначала положим dl, r = dl + 1, r, если мы не берем отрезки с левым концом в l. Если существует отрезок [l, r], мы обязательно включаем его в наше множество. Если мы берем другой отрезок, скажем, [l, i], где i < r, посмотрим на отрезки [l, i] и [i, r] (для них ответ уже посчитан) и попытаемся изменить значение dl, r. Асимптотика решения O(n2), потому что общее количество левых концов O(n). Затем необходимо вывести сертификат, т.е. само оптимальное множество. Это делается стандартным образом.
Задача D
Мухи НЕ могут видеть друг друга тогда и только тогда, когда они в противоположных вершинах. Существует несколько способов проверить это. Например, можно проверить манхеттенское расстояние |x1 - x2| + |y1 - y2| + |z1 - z2| = 3 или евклидово расстояние 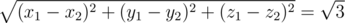 . Можно проверить, что все три координаты различны (x1 != x2) && (y1 != y2) && (z1 != z2) или просто (x1^x2)+(y1^y2)+(z1^z2) == 3!
. Можно проверить, что все три координаты различны (x1 != x2) && (y1 != y2) && (z1 != z2) или просто (x1^x2)+(y1^y2)+(z1^z2) == 3!
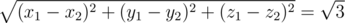 . Можно проверить, что все три координаты различны (x1 != x2) && (y1 != y2) && (z1 != z2) или просто (x1^x2)+(y1^y2)+(z1^z2) == 3!
. Можно проверить, что все три координаты различны (x1 != x2) && (y1 != y2) && (z1 != z2) или просто (x1^x2)+(y1^y2)+(z1^z2) == 3!Задача E
Количество способов разложить b предметов по a коробкам, конечно же, ab. У нас имеется ациклическая игра для двух игроков с состояниями (a, b), для которых ab < n. К сожалению, существует бесконечное количество таких состояний: a = 1, b любое. Но в этом случае, если 2b ≥ n, позиция является ничейной, потому что единственный способ действия для обоих игроков (не приводящий к поражению) - увеличивать b бесконечно.
Другой отдельный случай возникает для позиции с b = 1 и достаточно большого a. А именно, если 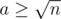 , имеется также только один ход из этой позиции - увеличивать a. Если a = n - 1, то позиция проигрышная, если a = n - 2 - она выигрышная, при a = n - 3 снова проигрышная и т.д.
, имеется также только один ход из этой позиции - увеличивать a. Если a = n - 1, то позиция проигрышная, если a = n - 2 - она выигрышная, при a = n - 3 снова проигрышная и т.д.
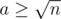 , имеется также только один ход из этой позиции - увеличивать a. Если a = n - 1, то позиция проигрышная, если a = n - 2 - она выигрышная, при a = n - 3 снова проигрышная и т.д.
, имеется также только один ход из этой позиции - увеличивать a. Если a = n - 1, то позиция проигрышная, если a = n - 2 - она выигрышная, при a = n - 3 снова проигрышная и т.д.Итак, имеется два вида состояний, которые нужно обрабатывать отдельно. Количество остальных состояний не очень большое, и для них можно вычислять стандартную динамику для игр на ациклических графах.
Задача F
Простое моделирование прыжков лягушек работает слишком долго, потому что n может быть 109. Правильное решение состоит в том, чтобы посчитать для каждой лягушки количество раздавленных комаров путем проверки делимости номеров кочек с комарами на di.
Задача G
Что можно сказать про задачу G? Нужно провести разбор данной функции и вычислить ее значение при всех значениях n. Разумеется, это невозможно сделать путем простой реализации рекурсии, потому что она может работать слишком долго (см. пример с последовательностью Фибоначчи). Поэтому нужно использовать динамическое программирование.
Задача H
Нужно вычислить все произведения i * j и вывести их в состеме счисления с основанием k.
Задача I
Рассмотрим только ту часть графа, которая достижима из вершины 1. Задача состоит в том, чтобы найти наибольшее такое t, чо выбранное множество вершин достижимо только в моменты времени, кратные t. Предположим, мы построили искомое множество S0. Рассмотрим множества S1, S2 ..., St - 1 всех вершин, достижимых в моменты времени, имеющие остатки 1, 2, ..., t - 1 по модулю t, соответственно. Нетрудно проверить, что эти множества не пересекаются и их объединение совпадает со всем множеством достижимых вершин. Ясно, что ребро из u в v может существовать только в том случае, когда u и v принадлежат последовательным множествам, т.е.  ,
, 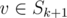 , k + 1 берется по модулю t.
, k + 1 берется по модулю t.
 ,
, 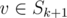 , k + 1 берется по модулю t.
, k + 1 берется по модулю t.Для каждой вершины v посчитаем расстояние dv от 1 до v (если существует несколько путей, выберите любой, например, с помощью обхода в глубину). Если из u в v существует ребро, должно выполняться 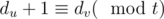 . Анализируя все ребра, мы приходим к заключению, что оптимальное значение t равно наибольшему общему делителю чисел |du + 1 - dv|. Теперь нетрудно райти множетсво S0.
. Анализируя все ребра, мы приходим к заключению, что оптимальное значение t равно наибольшему общему делителю чисел |du + 1 - dv|. Теперь нетрудно райти множетсво S0.
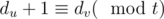 . Анализируя все ребра, мы приходим к заключению, что оптимальное значение t равно наибольшему общему делителю чисел |du + 1 - dv|. Теперь нетрудно райти множетсво S0.
. Анализируя все ребра, мы приходим к заключению, что оптимальное значение t равно наибольшему общему делителю чисел |du + 1 - dv|. Теперь нетрудно райти множетсво S0.Задача J
Самое простое решение - найти два числа l и r - длину наибольшего общего префикса и длину наибольшего общего суффикса двух строк, соответственно. Если l + 1 < n - r, решения нет. Здесь n - длина первой строки. Иначе нужно выдать позиции с max(n - r, 1) до min(l + 1, n).
Задача K
Задача К имеет огромное количество различных решений, поэтому мне удивительно, почему их было так мало во время соревнования. Проходили решения за
O(k4) и даже некоторые решения за
O(k5) с оптимизациями, но
KADR предложил решение даже лучше, работающее за
O(k3) (http://codeforces.net/blog/entry/793).
Здесь я приведу некоторые идеи жюри по этой задаче. В первую очередь сожмем координаты. Отметим по одной точке внутри каждого объекта и стандартной динамикой посчитаем количество отмеченных точек внутри каждого прямоугольника. Обработка всех возможных прямоугольников занимает O(k4). Возникает проблема с тем, что прямоугольник может содержать правильное количество объектов, но содержать некоторые объекты не полностью. Чтобы это предотвратить, проверим границы. Они являются отрезками, параллельными осям координат, и их количество O(k3). Поэтому мы можем предподсчитать, корректны они или нет, сравнивая их с каждым объектом. Затем нужно вернуться к несжатым координатам.
Следующее решение за
O(k5), и оно использует ограничение на количество объектов (3) в прямоугольнике. Обработаем все тройки объектов (то же самое, разумеется, для пар и до объектов по одному). Фиксируем тройку и заменим ее одним большим объектом. Затем будем двигаться от получившегося объекта вверх (и вниз), проверяя, может ли строка вверху (внизу) быть включена в пораженный прямоугольник. Для каждой строки выберем наибольший отрезок [l, r], содержащий текущий большой объект и не содержащий ничего больше. Используя эту информацию, нетрудно посчитать общее количество прямоугольников, содержащих данную тройку.











В задаче А можно было заменить K*(++а) на K*(a++)+K,итого имеем какую то сумму Ki+ сумму вида Pj*(a++),сортируем Pj по возрастанию и выводим ответ:)
а мы разделяли коэффициенты с постфиксной и суффиксной (или как их называют) формой, в каждом наборе сорт, и потом динамику за квадрат.
А можно увидеть 13й тест к задаче С ?
Заранее большое спасибо.
Если кому-то поможет - вот тест на котором моя программа работала неправильно:
8
4 3
5 3
9 3
9 4
9 5
13 4
14 4
15 4
Правильный ответ:
3
3 4 5
а может все таки когда достаточно большое число n? т.е. когда n > a^2
просто вашего случая вообще не может быть, так как условие :"Гарантируется, что изначальное количество способов строго меньше n.", а если a >= sqrt(n), то a^b > n!!!