Блог пользователя kenechi

Scaler Hiring Challenge Problems Discussion
Автор kenechi, история, 4 года назад, По-английски

Note :- The contest ended on 8 Aug

Here are the problems :-

Problem 1
Problem 2
Problem 3
Problem 4
Problem 5

It would be a great help if anyone could provide ideas about solving problem 3 and problem 5. Please share problems similar to problem 5 if anyone has seen such kind of problem before. Thanks

  • Проголосовать: нравится
  • +11
  • Проголосовать: не нравится

»
4 года назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится 
vector<vector<int>>th;
vector<int>child;
map<pair<int,int>,int>ed;
#define ll long long 
int mod  =(int)1e9+7;
map<pair<int,int>,ll>hw;
ll as  = 0;
void dfs(int u,int p=-1){
    ll ans  = 0;
    for(auto x:th[u]){
        if(x==p)continue;
        dfs(x,u);
        ans+=child[x];
    }
    child[u] = ans+1;
    if(p!=-1){
        int wh = ed[make_pair(p,u)];
        if(wh<=0){
            as= 1LL*(as%mod + 1LL*(1LL*(1LL*(wh+mod)%mod*(child[u]%mod))%mod+mod)%mod);
            as%=mod;
        }else
        hw[make_pair(p,u)] = 1LL*((1LL*wh%mod*(1LL*child[u]%mod))%mod+mod)%mod;
    }
}
int Solution::solve(int a, vector<vector<int> > &b, int k) {
    th = vector<vector<int>>(a+1);
    ed.clear();
    hw.clear();
    as=0;
    for(int i=0;i<b.size();i++){
        th[b[i][0]].push_back(b[i][1]);
        th[b[i][1]].push_back(b[i][0]);
        ed[make_pair(b[i][0],b[i][1])] = b[i][2];
        ed[make_pair(b[i][1],b[i][0])] = b[i][2];
    }   
    child = vector<int>(a+1,0);
    ll sum =0 ;dfs(1);
    vector<ll>v;
    for(auto x:hw){
        v.push_back(x.second);
   //    cout<<x.second<<" ";
    }
    
    sort(v.rbegin(),v.rend());
    ll j = v.size()-1;
   // cout<<as<<" ";
     sum =as;
    for(ll i=k;i<=j;i++){
        sum=1LL*(sum%mod+1LL*v[i])%mod;
        sum%=mod;
    }
    int ret = sum%mod;
    return ret;
}
}

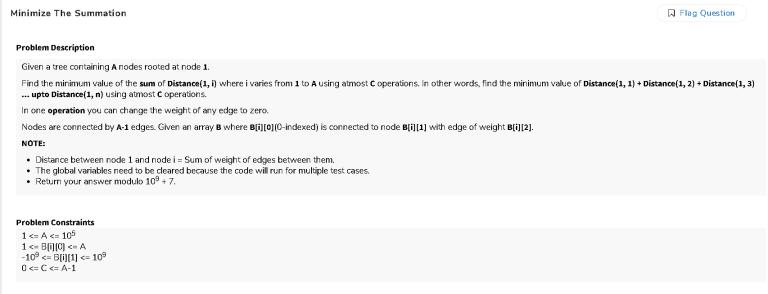
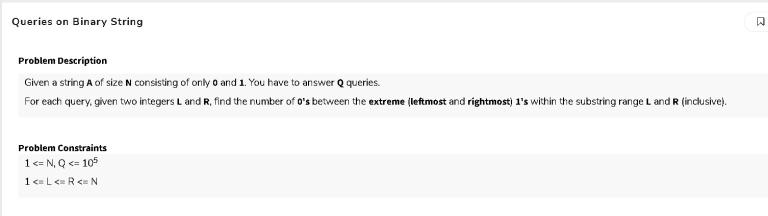
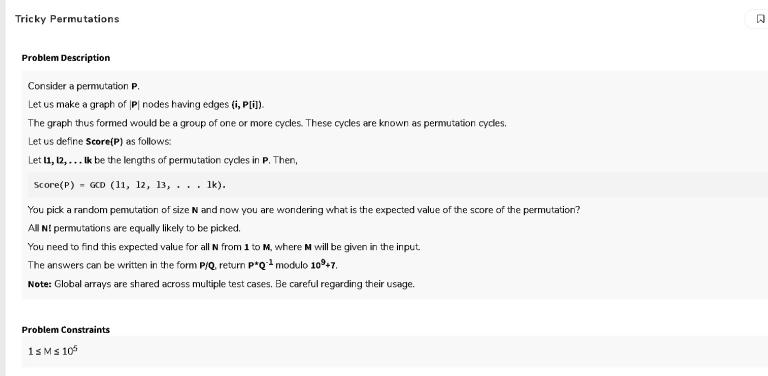
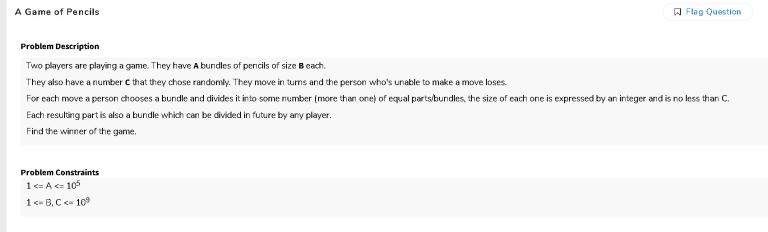
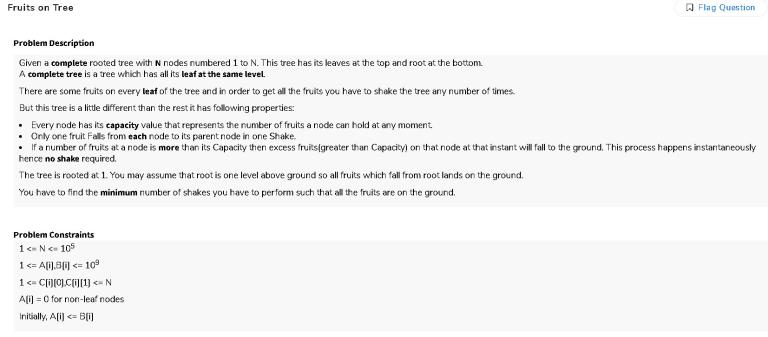
this was my answer to the first question but it was giving me only partial answer can someone tell me what's wrong with this pls I just check that how many times will we traverse an edge and if the weight of that edge is negative then we will never remove it and if it's positive I add it in array to calculate later so, at last, I have the array whose weights were positive multiplied by the time they will come and removed k from them

→ Ответить
  • »
    »
    4 года назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится

    Your logic is correct, I did the same, here's my code.

    Spoiler
    → Ответить
»
4 года назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

Where was this contest held ?

→ Ответить
»
4 года назад, # |
  Проголосовать: нравится +8 Проголосовать: не нравится

If possible post a text version, it is hurting my eyes when I try to read it

→ Ответить
»
4 года назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

can u also post the given test cases for problem 5.

→ Ответить
»
4 года назад, # |
  Проголосовать: нравится +4 Проголосовать: не нравится

Does anyone know how the 5th problem will be solved?

→ Ответить
»
4 года назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

Please post solutions/editorials of 3rd and 5th question.

→ Ответить
  • »
    »
    4 года назад, # ^ |
    ← Rev. 6   Проголосовать: нравится +10 Проголосовать: не нравится

    Tagging kal013 as he was the only one who solved third question,
    I referred generating function blog written by zscoder but I could only Calculate for specific n and small n(around 1000). I could not solve for each i from 1 to n, in the 3rd question,as it's very complex maths and also not available on oeis, so it might be some sieve related calculation
    Also tagging sudoBug,nagpaljatin1411 please help me here for 5th question.

    → Ответить
    • »
      »
      »
      4 года назад, # ^ |
        Проголосовать: нравится +3 Проголосовать: не нравится

      My 5th Question Approach:- Since all the leaf nodes were at same level, so we needed to see for how many seconds continuously a node would drop fruits(call it Ans of Node) [As there was no such case where it'd not drop fruits continuously]. While in a dfs, for a node, I calculated the [Sum] of fruits it recieved, and the [Max] number of fruit it recieved from all it'd children nodes. The Ans of a Node was [Max]-min([Sum]-[Max],it's capacity). You had to return Ans of Node[1] + the Depth of Leaf Nodes - 1.

      → Ответить
      • »
        »
        »
        »
        4 года назад, # ^ |
          Проголосовать: нравится 0 Проголосовать: не нравится

        The Ans of a Node was [Max]-min([Sum]-[Max],it's capacity). You had to return Ans of Node[1] + the Depth of Leaf Nodes - 1. I am unable to understand this can you pls explain.

        → Ответить
        • »
          »
          »
          »
          »
          4 года назад, # ^ |
            Проголосовать: нравится 0 Проголосовать: не нравится

          I'd explain by an example, You have a Node say i (which is not a leaf node) with it's children's Ans being 5, 8, 15 respectively. Now you know, that atleast for 15 seconds, Node i would constantly drop fruits, which leaves you with 13(15+8+5-15) fruits after 15 seconds. Now if your capacity is something less than 13, say 9, then fruits would fall for 9 more seconds (the 4 would fall directly to ground), else it'd fall for 13 more seconds. It doesn't matter, when the 4 fruits fall to the ground. Note that Ans of Leaf Nodes is equal to the Number of fruits they have i.e. A[i].

          Now for the Actual Answer which you had to return, The 1st Fruit from Leaf Node takes 'Depth-1' time to reach the Node-1, Now if Root was leaf Node, then Ans would have been Ans of Node-1, and if it's not, then the answer is Ans of Node-1 +depth-1.

          → Ответить
    • »
      »
      »
      4 года назад, # ^ |
      ← Rev. 2   Проголосовать: нравится +5 Проголосовать: не нравится

      My $$$O(Nlog^2 N)$$$ solution for problem 3:

      N here is the maximum limit for which all answers have to be found.

      Let $$$f(n,g)$$$ be ways of choosing permutations such that each cycle length is a multiple of g. Let $$$h(n,g)$$$ be ways such that gcd of the cycle lengths = $$$g$$$.

      The final answer is the $$$ \sum_{g=1}^{n} g * h(n, g) $$$ for any $$$n$$$ ( $$$h(n, g) = 0$$$ if $$$g$$$ does not divide $$$n$$$).

      Now we have the following relation:

      $$$\sum_{k=1}^{\frac{n}{g}} h(n,k*g) = f(n,g) $$$

      If we are able to calculate $$$f(n,g)$$$ over all pairs $$${g, n}$$$ such that $$$g | n$$$, then we can calculate $$$h(n, g)$$$ in $$$O(N log ^ 2 N)$$$, by noting that for each $$${g, n}$$$:

      $$$h(n, k*g)$$$ is $$$0$$$ if $$$k*g$$$ does not divide n or $$$k$$$ is not a divisor of $$$\frac{n}{g}$$$.

      So by iterating only over factors of $$$\frac{n}{g}$$$, we can see that for each $$$g$$$, number of steps taken will be

      $$$\sum_{i=1}^{\frac{N}{g}} numberOfFactors(i) = O(\frac{N}{g} log \frac{N}{g}) $$$

      Summing this over all g, we get the desired complexity.

      Now to calculate $$$f(n,g)$$$, choose size of cycle containing $$$n$$$. If the size is $$$k*g$$$ then ways =

      $$$\binom{n - 1}{kg -1} * (kg -1)! * f( n - kg, g) = (n - 1)! * (\frac{f(n - kg, g)} {(n - kg)!})$$$

      $$$f(n, g) = \sum_{k = 1}^{\frac{n}{g}} (n - 1)! * (\frac{f(n - kg, g)} {(n - kg)!})$$$

      This can be computed in $$$O(N log^2N)$$$ by using the previous trick or in $$$O(N log N)$$$ by maintaining a running sum of $$$\frac{f(n - k*g, g)}{(n - k *g)!}$$$

      → Ответить
  • »
    »
    4 года назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится

    EnEm zeus_iitg please help us with 3rd and 5th question.

    → Ответить
  • »
    »
    4 года назад, # ^ |
      Проголосовать: нравится +5 Проголосовать: не нравится

    For the 3rd problem, evilbuggy described a solution that solves for a fixed $$$N$$$ (not for all $$$N$$$ from $$$1$$$ to $$$N$$$) in $$$\mathcal{O}(N \log n \cdot \mathtt{div} N)$$$.

    text
    img
    → Ответить
»
4 года назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

Where is the ranklist?

→ Ответить