Задача E. "Ну-ка, покатились!"
Рассмотрим решение с помощью метода динамического программирования.Пусть Di - минимальный штраф, который мы заплатим, если будем решать задачу для шариков с номерами от i до n, причем шарик номер i будет обязательно приколот.
Тогда
где
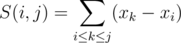
Если числа S(i, j) не считать каждый раз, а пересчитывать, используя формулу S(i, j) = S(i, j - 1) + xj - xi, то решение требует всего O(n) памяти и O(n2) времени на решение.
Важное замечание: в приведенных рассуждениях, шарики нужно рассматривать в порядке увеличения их координат.











Let $$$dp[i][0]$$$ be the minimum cost of reaching ith coordinate such that ith coordinate is pinned. and let $$$dp[i][1]$$$ be the minimum cost of reaching ith coordinate such that ith coordinate is not pinned. and let $$$dp[i][2]$$$ be the number of balls free for sliding at $$$i^{th}$$$ coordinate. Then suppose $$$dp[i][0] = min(dp[i - 1][0], dp[i - 1][1] + dp[i -1][2] * dist) + cost[i]$$$
and if $$$dp[i - 1][0] > dp[i - 1][1] + dist * dp[i - 1][2]$$$ then $$$dp[i - 1][1] = dp[i - 1][0]$$$ else $$$dp[i - 1][0] = dp[i - 1][1] + dp[i - 1][2] * dist$$$.
TLDR; I couldn't find bugs in my proof, any help highly appreciated! Also, can anyone prove the greedy algorithm? Thanks!