We hope you liked the problems. See you on day 2 :D
Problem A
Problem B
Problem C
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3857 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3463 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 166 |
| 2 | -is-this-fft- | 161 |
| 3 | Qingyu | 160 |
| 4 | Dominater069 | 159 |
| 5 | atcoder_official | 157 |
| 6 | adamant | 155 |
| 7 | Um_nik | 152 |
| 8 | djm03178 | 151 |
| 9 | luogu_official | 150 |
| 10 | awoo | 148 |
| Name |
|---|



Problems were really good.
i use the same approach as mention in tutorial A but scores only 12 points, will someone help me to find out the bug?
try multiplying by inverse of 2 instead of dividing by 2, that could be the issue.
UPD : inverse of 2 is $$$2^{MOD - 2}$$$
I dont think so since x*(x+1) is always divisble by 2
It's not about whether it's divisible or not, when you're using mod you shouldn't perform division. For example, try computing n choose k with mod and dividing and then try it using inverse modular.
" x *= (x + 1); x /= 2; x %= M2; " He uses mod after dividing which works here just fine.
Oh you're right, sorry didn't pay attention.
For 2 inverse is always (MOD+1)/2 if it exists.
I believe you can overflow int64 in
getbecausexcan be as large as $$$10^9 \cdot n$$$?Yeh, that seems to be the problem.
C can also be solved with all-directions DP + matrix fast pow: For the last layer ($$$i = D$$$), we compute for every edge $$$u \to v$$$ whether the state we get after moving from $$$u$$$ to $$$v$$$ is winning. This allows us to compute for every vertex whether starting at this vertex is a winning state in $$$O(n)$$$ time in total. Let's call those vertices winning vertices.
Let an $$$i$$$-configuration be a way of placing the tunnels between layers $$$i, i+1, ..., D$$$. (In particular, the total number of $$$i$$$-configurations is $$$n^{2(D-i)}$$$.) When considering tunnels from $$$i$$$ to $$$i+1$$$, we only care about whether this tunnel leads to a winning vertex or not. We compute for every edge $$$u \to v$$$ the number of $$$i$$$-configurations for which the state we get after moving from $$$u$$$ to $$$v$$$ is winning/losing and for which the tunnel is reachable from $$$v$$$. This in turn allows us to compute for every vertex in layer $$$i$$$ the number of $$$i$$$-configurations for which this vertex is winning in $$$O(N)$$$ time in total. Doing this for all $$$i$$$ gives an $$$O(D N)$$$ time algorithm.
To get $$$O(N + \log D)$$$ time, note that total number of winning/losing vertices in layer $$$i$$$ among all $$$i$$$-configurations depends linearly on the total number of winning and the total number of losing vertices in layer $$$i+1$$$ among all $$$(i+1)$$$-configurations. Hence we only have to run the dp three times: Twice to get the matrix of this linear map and once for the first layer (as the starting vertex is fixed). (It is also possible to avoid the third call.)
In problem C, subtask 5, I don't really get the ''we can reroot the tree easily'' part and I've complicated myself with if's and all that.. Could someone please help me?
Figured it out, because when you go father->son the father becomes son's son (ironically), you can have another variable ver in dfs which is what father's state would be as a son (pretty complicated but it's late and I can't think straight), and ver is state[father] unless state[father]=1 and he has only one son with state=0 (the number of sons with state 0 is |{state[son]=0}|+(ver=0) because ver is also a son!) and state[son]=0, in which case ver=0 because the father's state becomes 0, having only 1's as sons, AND state[son]=1. A few observations are that you need to copy the states vector since you will need it later in another dfs and ver is initially 1 because why not :)
I wrote this in case anyone else had this problem for them not to spend a lot of time with 1's and 0's going crazy in their heads XD
Sorry for not using Codeforces syntax but I don't know any of it
Guys could you tell me why do i get tl on subtask 6? Code
Can someone help me find bug in my code, it is for subtask 4 of Problem A. 91100908
Put code in pastebin and provide link here.
https://pastebin.ubuntu.com/p/5w4Sr3D6zn/
Here is the code in python
https://ideone.com/Ta14yb
const's value should be (mod + 1) / 2
w = w % mod
Thanks for helping. I was not taking the mod when summing widths.
Can someone explain the Problem B sweep line more in detail, I don't really understand what the author means by Rmost(u), how is it calculated, and how it helps us in building the tree.
Let me a try. When sweep line move along the plane there are current lines, past lines and future lines. Past and current lines are already connected to tree.
When sweep line intersect new future line it should be connected to one of the current or past line. We can't connect it to the right end of the current line (it can intersect future line) and we can't connect it to the left end of the current line because it can intersect past lines. But if we store rightmost end of the past line then it can't intersect with any other line. Let's store past rightmost end of the past lines between current lines. When we connect line to the past or current line the left(!) point of added line become new rightmost point for sectors above and below added line. And connected line become current line.
And now with picture :)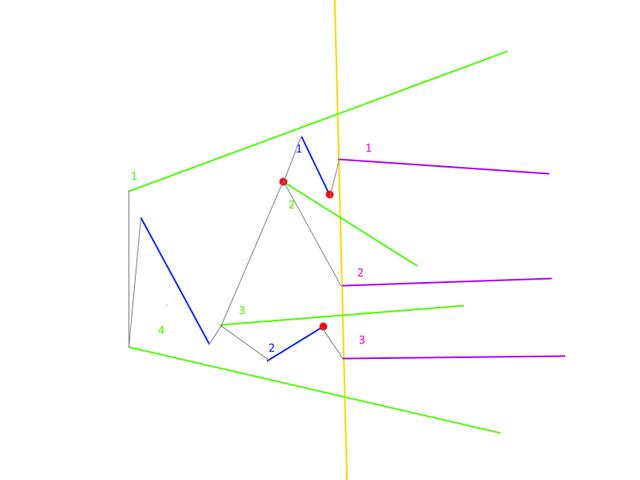
The rose is red, the violet’s blue ... sory another picture. :) Rightmost points are red. Past lines are blue. Current lines are green. Future lines are purple.
For purple line 1: Current lines are 1 and 2. The Rightmost point is end of the blue line 1. Connect purple line 1 to blue line 1 and add purple one to current lines. Left point of purple line 1 is a new Rightmost point for sector between green 1 and purple 1. Also Left point of purple line 1 is a new Rightmost point for sector between green 2 and purple 1
For purple line 2: There is no past lines between green 2 and green 3 so the Rightmost point is left point of green 2 (it was added later than green 3). Connect and update left point of purple 2 is a Rightmost for green 2 — purple 2 and purple 2 green 3.
For purple line 3: The same as for purple 1. Connect purple 3 to blue 2 and left point of Purple 3 is a new rightmost point for green 3- purple 3 and purple 3 — green 4.
I tried ... sorry :)
In Problem A, I am not able to understand why my solution is not working. It has only passed Subtask 2. I dont know why it does not work on all subtasks. A little help would be really appreciated.
So , What I have tried is to store for each height element the closest index of an element lesser than it in the forward direction and the closest index of an element lesser than or equal to it in the backward direction (using a stack). Considering a fancy rectangle as just the bottom left corner and the top right corner, all fancy rectangles can be actually considered to be part of pairs of fences. So, then for each element in height array, I counted all possible pairs of fancy rectangles from the backward part to the forward part . Clearly, for all such pairs the upper limit for the height of the upper edge of the rectangles is the current element of height array in consideration. Knowing the maximum possible height, I can easily calculate the fancy rectangles by assuming something like merging the forward and backward parts and then removing those fancy rectangles that lie in the same part (using Combinations Formula). Cases left to handle are when combining the current element with the forward or the backward part (done similiarly), and the fancy rectangles that are present in current height itself. However, Only Subtask 2 is being Accepted. Here is my commented code.
Oh! yellow_13 helped me figure out. Actually, I had over seen a modular mistake and also, wherein I was multiplying two elements of prefix sum as (pref1*pref2)%mod which may give overflow. There were some other problem with the way I was writing code too.
I read the editorial of problem B. It's a good approach. But I didn't understand how can we find for every point q such points v, u that q is located between v and u. Could anybody please help me with that?
After 3 days of trying to get the last subtask of problem A. I finally solved it with segment tree lol.
Why aren't you maintaining a prefix :o
I solved A in Linear time complexity using Stack(By precalculating the next smallest element in left and right). But not able to understand how DSU or sorting can be used to solve this problem.
Can somebody explain how DSU more clearly? How we are able to get sum of widths from x to yth node using dsu?
Hi! Can you please explain your solution using stack? Is it different from the editorial?
REDACTED
Problem $$$A$$$ was cool, cannot speak about the others since I didn't solve yet :P
I have a different solution.
Observation 1: The number of fancy rectangles in an $$$H \times W$$$ rectangle is $$$\binom{H + 1}{2} \cdot \binom{W + 1}{2}$$$.
This is true if we imagine fixing the two vertical axes of the rectangle (there are $$$(W + 1) \cdot W/2$$$ ways to do so) and then fixing the two horizontal axes of the rectangle (there are $$$(H + 1) \cdot H/2$$$ ways to do so). We divide because one of the axes will be lower than the other.
Observation 2: We can fix indices $$$(i, j)$$$ and find the number of rectangles that partially contain i and j but not i — 1 and j + 1.
Assume $$$i \ne j$$$. If $$$i = j$$$, resort to observation 1. Suppose that the minimum height from $$$i \to j$$$ is $$$H$$$. Then, we have $$$\binom{H}{2} \cdot w[i] \cdot w[j]$$$ ways to fix the rectangle. This is because we can fix the widths in $$$w[i] \cdot w[j]$$$ ways and the height in $$$\binom{H}{2}$$$ ways. This gives 30 points: 146963809, if implemented naively in $$$\mathcal{O}(N^2)$$$.
Observation 3: We can fix the minimum height $$$H$$$ on the interval and do black magic from here :P
We fix our minimum height $$$H$$$ and fix the leftmost index $$$ind$$$ which has that height. This can be done via a map in $$$\mathcal{O} (N \log N)$$$. Now, we want to find $$$\sum w[i] \cdot w[j]$$$ where $$$(i \dots j)$$$ contains $$$ind$$$ as the leftmost index with minimal height. This is a very standard problem, I've seen at least 3 variations.
We first want to find the leftmost index $$$L$$$ for which $$$\min_{L \to i} \ge H.$$$ This can be done via sparse table or segment tree and binary search. Analogously, we can find rightmost index $$$R$$$ for which $$$\min_{i \to R} > H$$$. Now what? Okay, so given $$$L, R$$$, we actually want to evaluate the sum
This can be done via prefix sums easily.
The end.
It's pretty easy I think, once you make observation 2. Code is not too bad 146970245
Your link of code is not visible.Can you do it visible?
Can anyone help me with my pA's solution? I could only get 15 points https://ideone.com/pagI2z