This post is about memory requirements for fast range queries.
First, let's consider 2 following types of queries on a sequence x[0]..x[n-1] in O(logn):
- sum(a, b) — calculate x[a] + x[a+1] + ... + x[b]
- add(i, value) — x[i] += value
This is a well-known problem that can be solved using Fenwick tree.
What is good with Fenwick tree — is that it gives memory-optimal solution in the sense that it needs an array of only n elements, where each element has enough capacity to store any sum(a,b). Unlike Fenwick tree, any solution based on segment tree will use at least 2*n elements.
Now suppose we need range update and our query types become the following:
- sum(a, b) — calculate sum x[a] + x[a+1] + ... + x[b]
- add(a, b, value) — x[a]+=value x[a+1]+=value ... x[b]+=value
This is most often solved using segment tree with 2 arrays (something like sum[] and delta[]), each of 2*n or 4*n size. So the minimum memory consumption is 4*n which is far from optimal n.
We can improve. It was discovered that Fenwick tree can be altered to support both range queries and updates. All following solutions use 2*n elements:
- Petr blog: http://petr-mitrichev.blogspot.ru/2013/05/fenwick-tree-range-updates.html
- Topcoder forums: link1 link2
- habrahabr.ru (russian only): http://habrahabr.ru/post/170933/
However there is also a solution with segment tree that seems to work, but I don't have a prove. We leave only array sum[] and while walking down the tree we push delta = sum[i] — sum[2*i+1] — sum[2*i+2] down. He is source code, which is not quite honest though, because it achieves 2*n consumption only if n is 2m - 1. But is seems that non-recursive segment tree solves the problem.
So, listed variations of Fenwick tree do not improve over segment tree here and all use 2*n elements.
Can we prove that a single Fenwick tree with n elements is not enough to process both range queries and updates in O(logn)?











Here's an algorithm which uses exactly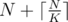 words of storage for some constant K, by compressing one of the Fenwick trees into N/K words and performing at most 2*K-2 extra O(logN) updates per insertion: (pastebin)
words of storage for some constant K, by compressing one of the Fenwick trees into N/K words and performing at most 2*K-2 extra O(logN) updates per insertion: (pastebin)
Impractical, yes, but it proves that 2N is not the lowest bound possible.