Given $$$N$$$ points in $$$2D$$$ plane with integer coordinates. Initially you are at a point $$$p1$$$ , visit all remaining $$$n-1$$$ points and come back to $$$p1$$$ . Between two points you move in a straight line joining them . Only constraint is that no two of the lines must intersect .
Constraints:
$$$3 ≤ N ≤ 1000$$$
$$$-1,000,000 ≤ x i , y i ≤ 1,000,000 $$$
Problem Link — Mission-Infoarena
Some help is appreciated as im stuck so bad.
UPD: Solved
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
17:57:40
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
17:57:40
Зарегистрироваться »
*есть доп. регистрация
→ Трансляции
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 23:37:20 (j2).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











use the onion-decomposition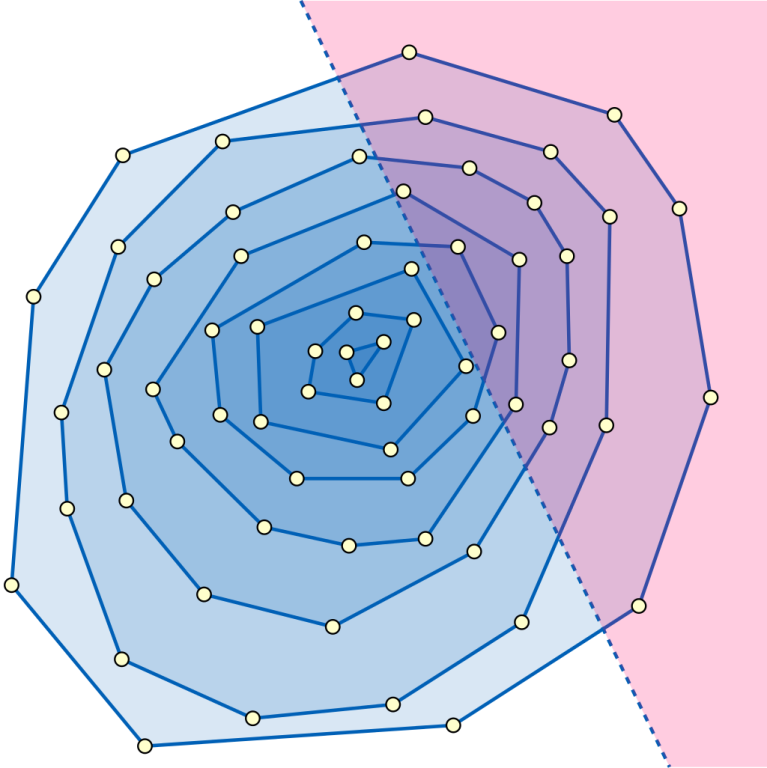
We need to come back to the point we started from, Is it possible moving this spiral way? Also, the starting point is fixed( first point in the input) .
if you are at a point p1 and you want to go to another spiral (the one above or below it) you should find the closest point in that spiral to p1 and go to it, try to work by hand some examples and you will see it's always possible no matter where you start.
I just realised , the complexity will be $$$O(n^2)$$$ . Thanks for the help.
You forgot to mention the constraint that no three points are collinear. Pick the leftmost point and put it as the first point, then sort all other points by angle, and visit them in this order.
Sorry, my bad. Btw, nice observation