Today at 11:00 AM EDT will SRM 585. Lets discuss problems here after end of the contest.
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
19:11:11
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
19:11:11
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 22:23:49 (l1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











Updated compilers and added Python compiler!
But they failed to provide it during contest time. Hope good luck for next time.
I coded in c++ and have +220. Feeling WOW!!
(ignore)
Who can't see pictures?
UPD: fixed, sorry.
In Div1 250 the answer is [(2^(N+1)-1)/3] +1*((2^(N+1)-1) % 3 !=0). However everybody in my room got something like dp solution. What's the logic of dp solution here?
It is easy to see that you need send car from left leaf to second left, from third left to fourth left, and so on. So, two bottom levels are removed, and repeat.
UPD: And so we have something looks like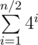
I had the same thoughts, but derived formula instead of doing easy calculation with arrays :(
Yeah, I did the same. That was my quick idea I got from the example tests' pictures.
its dp[0]=1; dp[1]=1; for all i=2 to n dp[i]=dp[i-1]+2*dp[i-2];
its Jacobsthal sequence sequence http://oeis.org/A001045
Alternatively:
If you run one car from the leftmost leaf to the rightmost leaf of the tree, what's left is a sequence of pairs of smaller trees with heights 0,1,..,treeHeight-2.
When I run applet it always unable to launch. I go to topocder but the page can't be access. I can only launch applet at half of contest and in challenge phase I was kicked out of applet. Anyone tell me it topcoder's error or my network's error?
Ну вот кому нужен был этот вырожденный случай в 1000? Я, конечно, понимаю, что скорее всего это исправляется всего одним неравенство в условии перехода указателей, но тем не менее(
А можешь описать идею в общих чертах?
Мы будем классифицировать каждый треугольник по вершине с наименьшим номером.
Сначала двумя указателями можно за O(x.size()*m) предподсчитать для каждой вершины ее "касательные" к множеству черных точек (нас волнует в какие красные вершины она упадет).
Дальше три указателя. Понятно я это объяснять не умею. В общих чертах примерно следующее. Мы зафиксировали вершину А. Вершина B идет в обходе квадрата после A, а вершина C до нее. Мы поддерживаем инвариант, что все черные точки лежат в угле CAB и считаем треугольники такого типа. Дальше каждый раз когда мы двигаем одну из точек мы знаем какое количество треугольников мы выкидываем или добавляем из предподсчета с двумя указателями. Границы сдвигания берутся оттуда и от того, что мы не должны случайно посчитать треугольник дважды (например, чтобы вершина A имела наименьший номер).
Я не претендую, что это строго и уж тем более понятно, но общую мысль, я надеюсь, я смог донести.
Ну да, примерно понятно, спасибо.
Сорок минут потратил на то, чтобы решить 500 с другой формулировкой. Подумал, что мы не конкатенацию возрастающих последовательностей берем, а сливаем их в произвольном порядке.
Кстати, правда ведь, что задача "на сколько возрастающих подпоследовательностей можно разбить последовательность" в этом смысле сама по себе за квадрат не решается никак?Оказывается, решается.о, я только после прочтения коммента понял что тоже решал не то
Задача "на сколько возрастающих подпоследовательностей можно разбить последовательность" решается за n log n, ответ — длина максимальной невозрастающей подпоследовательности.
"На сколько" это просто длина наибольшей убывающей подпоследовательности.
Теорема Дилворта тогда.
Её можно и без переформулировки решать. Надо просто идти слева направо и поддерживать множество последовательностей на которые разбит префикс(оптимальное), а дальше жадно добавлять куда можем(кстати такой алгоритм даёт и наибольшую неубывающию последовательность)
А как решается с оригинальной формулировкой?
n^5 должно заходить, но я, видимо, что-то неэффективно написал. dp[i][j] — кол-во способов составить последовательность из чисел <= i, так, что будет j перегородок между группами (или j+1 групп). Переход — добавление всех чисел, равных i+1. Мы их делим на α групп (фиксируем). Группы будут располагаться подряд. тогда это добавит X - α перегородок само по себе. Группа может лечь туда, где уже есть перегородка, это ничего не меняет. Может лечь туда, где не было перегородки или в начало (это добавляет по одной перегородке для каждой положенной группы) и в конец (ничего не добавляет). Надо перебрать сколько ложится на существующие разрезы и ложится ли что-то в начало. Дальше пишем несколько цешек и переходим.
Это действительно проходит, только не рассматривать начало и конец, как отдельные варианты.
Немного напоминает.
Немного по-другому можно за O(N^2*K). Тоже динамика, состояние это [текущее число][количество доданных текущих чисел][количество групп]. Различие в тому, что каждый элемент рассматривается отдельно (а не группами), поэтому как-бы порядок одинаковых чисел становится важным, то есть в конце нужно поделить на факториалы.
oeis is your friend as well :)
same here I used OEIS :)
can someone explain how to solve DIV2 1000?
step 1 . choose 3 color
step 2 . choose 1 point for each 3 color O(n^3)
step 3 . check them . if this triangle covers black points increase ans ;
in step 3 if u dont know how to check any point is inside the triangle trick is if any pair of points in triangle (p1,p2) if ccw(p1,p2,p3)!=ccw(p1,p2,point) point is outside else inside
more eficient way is choose 2 points and use binary search for 3.point or another way is for each pair of colors find pair of points that not divides black points O(n^2)
Do you mean that complexity of your solution is O(number_of_black_points * m^3) ?
no there is a paragraph that explains eficient solution.
can you plz expalin this condition : ccw(p1,p2,p3)!=ccw(p1,p2,point) What is CCW ?
CCW means counterclockwise.
ccw(p1,p2,p3)!=ccw(p1,p2,point) means that the arcs p1-p2-p3 and p1-p2-point do not rotate in the same direction.
Here is another algorithm in O(MMN). I observed that for all valid triangles, two of the three pairs of the vertices are chosen from the two perpendicular sides of the M*M square. Thus we can count them by going through all pairs of the two vertices on the sides colored (R, G), (G, B), (B, Y), (Y, R). For each pair, we can check if it can contain all the points in O(N) and also count the number of the possible third vertices in O(lgM) by using binary search to find the boundary of the possible third vertices on the other two sides of the M*M square. So in the end, the total needs to be divided by 2, because we double count each triangle.
Div 1 500 was a quite interesting DP. Unfortunately I couldn't fix my bug in time (2 lines misplaced T T).
Help me please. I was participating from my PC, but then electricity fell down. I took laptop, but arena wasn't working on it. It says "Unable to launch the application". What is the reason of problem?
Yesterday I had the same problem. I've cleaned java cache (found this tip at topcoder forum).
Nice problems ! :D
I'm not sure, but I think another recursion that could be found is an = 2n - 1 + an - 2. It gives the same result as the other recursion.
My approach to find this recursion was to use one car for each of 2n - 1 binary trees of height 1 at down of tree, so the tree without them would be a binary tree with height of firstHeight - 2.
Can someone mention the idea behind using Jacobsthal sequence in this problem, or it's just a consequence?
Editorial