neo999's blog

Find OR Sum of the Range
By neo999, history, 4 years ago, In English

You are given following:- - an array A consisting of N positive integers - Q queries of the form L,R,M

consider all subsequences of subarray from L to R of size M.

Determine the sum of Bitwise OR of all these subsequences. Bitwise OR of an empty subsequence is 0. If there is no Subsequence of Length M, print 0.

  • print the output with mod 998244353.
  • A subsequence is a sequence that can be derived from the given sequence by deleting 0 or more elements without changing the order of the remaining elements.
  • 1 based indexing is followed.

Example A=[1,2,3] Q=[1,3,2] // L,R,M

subarray= [1,2,3] for this we have 3 subsequences of length 2. - [1,2] [2,3] [1,3]

Bitwise OR of all above subsequences is 3+3+3=9 , so output is 9

constraints as below

  • Vote: I like it
  • 0
  • Vote: I do not like it

Comments Comments (3)
| Write comment?
»
4 years ago, # |
  Vote: I like it +18 Vote: I do not like it

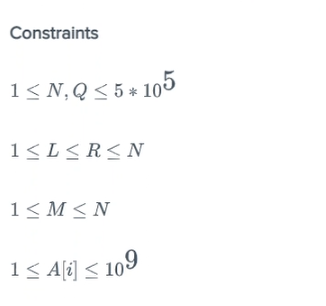
Operate on each bit separately. For ith bit = ((r-l+1,m)-(# off bits,m))*2^i , where (a,b) is binomial coefficient.

→ Reply
  • »
    »
    4 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Hi could you elaborate little more? i m kind of beginner, so could not connect much. may be small example would be useful. thanks

    → Reply
    • »
      »
      »
      4 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Let's rephrase this problem , consider a binary sequence [0,0,0,1,1,1] how many sub sequences exist of a given sequence having length m such that it contains at least single 1 ?? (# sub sequence of length m — # sub sequence containing only 0)

      → Reply