Просто считать динамику от 3 параметров (сколько осталось, сколько у первого, сколько у второго). Значение динамики — маск. выигрыш, переходы — все, которые возможны по условию.

No, it will not. you can't see other people code in CF gym before get AC for this problem

Because you can only view a solution after you've solved a problem. It's really tiring to write this every time...

L: Key observation: ans(L, R) = ans(1, R) — ans(1, L — 1).
So one can iterate over the number of ones in binary representation(let's call it C). If the current number of ones gives proper X value, then all what we need to do is to calculate the amount of numbers which have exactly C ones in binary representation and less or equal to R.
One can do this using dynamic programming(the state is (number of bits processed, number of ones used, is it equal to or strictly less than R)).

D: Let's say that team i gets x_i balloons of type A and K_i - x_i of type B. Then, the cost for that team is C_i = D_A, ix_i + D_B, i(K_i - x_i) = D_B, iK_i + x_i(D_A, i - D_B, i). We need to minimize .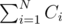

The first term is constant, so let's ignore it. Then, we can sort the teams and use a greedy approach: go from smallest D_A, i - D_B, i to largest. As long as D_A, i - D_B, i < 0, we give the team as many balloons as possible, so that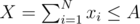 and x_i ≤ K_i. Once we move on to D_A, i - D_B, i ≥ 0: for a valid solution, we need 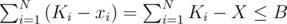, but we don't want to increase X anymore when that's valid, because it increases the result. So if we can achieve that condition's validity by setting x_i to some value  ≤ K_i for some i, we do it; otherwise, it's best to set x_i = K_i.

It needs careful checking of all conditions' correct combinations, but no extreme algorithms otherwise. Total running time: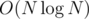 per test case.

L: Observe that after the first iteration, any number will drop to at most 60, because there can be at most 60 ones in its binary representation. So we need to be able to calculate 2 things: "for given A and k, how many numbers in the interval [1, A] have exactly k > 0 ones in binary?" and "how many iterations does it take to get to 1 from k"?

The second part is easy, just bruteforce it. The first is quite tough. Number the bits of A as b_0..m, where b₀ is least significant. We go from b_m to b₀. For every bit, we have at most 2 choices: either the numbers we're interested in will have bits b_i to b_m equal to those of A, in which case we just continue on, or (only possible if b_i = 1) we have the numbers with b_i = 0 and all larger bits equal to those of A; those numbers will all be  < A, so there is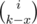 of them, where 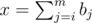. So we need to calculate binomial coefficients up to around 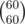. That works in 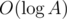. Now, we can try all possible k, find out how many times we'll have number i after one iteration, and count how many of those take X - 1 more iterations to get to 1.

EDIT: Whoops, already answered. At least I've got a more detailed (and more chaotic :D) explanation.

А расскажите, пожалуйста, как решать A, C и E :)

И G :D

Greedy: sort the intervals by their ends, then process them in increasing order. Always add as few points into the set as necessary for the condition of that interval to be valid, and take them from the last one that you still haven't taken (that ensures that they intersect with as many of the unprocessed intervals as possible).

There are at most 50000 points to be added, so store them in a set. To find out how many points from the set are in an interval, use a Fenwick tree (BIT) for sums.

One can solve this problem with next greedy algorithm. Let's sort segments in increasing order of right end. When processing i-th segment let's see how many integers from that segment are already taken. If we have taken x integers from that segment and x < c_i, we still need to add some numbers into set. Let's do that starting from the right end of the segment r_i in decreasing order.

You may need some data structures for this solutions, for me it was enough to use set to store unused numbers and Fenwick tree for checking how many integers there are already in segment.

UPD: Xellos was faster =)

Let's sort our intervals [a;b] by b. Consider the first interval [a1;b1]. Obviosly, we must put points in positions {b1, b1-1, b1-2, ..., b1-c1+1}, because it will be better for future intervals. Now delete the first interval and continue our algorithm. If interval [ai; bi] has already ci points we do nothing. So, we need to find sum on a interval [ai; bi] and to put a points in the end of out interval. We can keep Fenwick tree and set with unused points. My implementation : http://ideone.com/NMYH6F UPD : Xellos and Zlobober were much more faster than me :D

That's an easy one. Realize that we can split a palindrome of length L into 2 halves, of lengths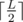 and 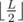, where the 2nd one is uniquely defined by the first. We only need to consider 2 possibilities: either the result's first half is equal to the original string's first half (in which case the result might be a smaller palindrome and then it's not valid), or it's just larger by 1 (in which case it's definitely a larger palindrome); construct those 2 and choose the smaller one larger than the original string.

Dynamic programming. A state DP[i][j][k] is the maximum number of donuts Steve can eat, if there are i donuts in the box, Steve has j and Digit k donuts, and it's Steve's move. (If it isn't Steve's move and, he can eat i + j + k - DP[i][k][j] donuts — applying the optimal strategy for Digit.) Time O(N⁴).