Задача A
Задача решается простым моделированием описанного процесса. Главное - правильно обработать переход через n. Это можно сделать либо взятием номеров по модулю n (с прибавлением 1), либо вычитать n каждый раз, как текущий номер стал больше n.
Задача C
Сначала посчитаем, сколько в последовательности хомячков. Пусть их h. Переберем позицию, в которой будет начинаться последовательность хомячков, и для каждой начальной позиции посчитаем, сколько тигров оказалось в отрезке h, начиная с этой позиции. Этих тигров придется поменять с хомячками за количество обменов, равное количеству тигров, стоящих не на своем месте. Выберем минимум по всем начальным позициям.
Задача F
Во-первых, заметим, что все описанные операции (открытие/закрытие дверей, перемещения из одной комнаты в другую, обмен ключами) обратимы. Поэтому можно применить несколько таких операций из начального расположения и получить некоторое расположение A, и затем получить то же расположение А путем применения подобных операций из конечного расположения, в этом случае ответ будет "YES". Применим следующую стратегию к обоим расположениям: пока существует человек, который может перейти в некоторую комнату и открыть некоторую дверь, выполнять это действие. В результате для каждого из расположений мы получим связные подмножества комнат (будем называть из связными частями дома), соответствующие подмножества людей и ключей в каждой связной части дома. Если результирующие подмножества совпадают для начального и конечного расположения, то ответ на задачу "YES", иначе ответ "NO". Действительно, в случае совпадения можно очевидным образом из начального расположения получить результирующее, а из него - конечное. В противном случае это невозможно сделать, потому что найдутся ключи, которые не могут быть применены к соответствующим дверям, находящимся в другой связной части дома, или найдутся люди, которые не имеют возможности проникнуть в комнаты, расположенные в другой связной части дома.
Во-вторых, несколько слов о реализации. Один из возможных способов - хранить две булевы матрицы
1) определяющую для каждого человека, может ли он попасть в каждую из комнат, и
2) определяющую то же самое для каждого ключа,
и рекурсивно выполнять операции:
1) если человек может оказаться в комнате, попробовать сделать переходы в соседние комнаты,
2) то же самое для ключей, пытаясь при этом открывать дверь в соседнюю комнату,
3) когда дверь открывается, сделать переход для людей и ключей в смежных комнатах.
Таким образом, мы перебираем каждую пару человек-комната, человек-дверь, дверь-ключ, дверь комната O(1) раз, поэтому общая асимптотика решения O(nk + km + m2 + nm).
Задача G
Заметим, что длинами сторон могут быть числа 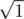 ,
, 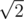 ,
, 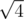 ,
, 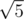 и т.д., т.е. корни целых чисел, представимых в виде a2 + b2. Сгенерируем достаточное количество таких чисел. Обозначим их
и т.д., т.е. корни целых чисел, представимых в виде a2 + b2. Сгенерируем достаточное количество таких чисел. Обозначим их 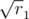 ,
, 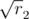 , ... В некоторых случаях можно взять в качестве длин сторон первые n чисел, но в некоторых случаях этого сделать точно нельзя. Все зависит от четности. Если сумма r1 + r2 + ... + rn нечетна, это невозможно сделать. В самом деле, каждую сторону можно представить вектором (xi, yi), xi2 + yi2 = ri (xi и yi могут быть отрицательными). Если число ri четно, сумма xi + yi также четна. Если ri нечетно, то и xi + yi нечетно. Если можно построить многоугольник с векторами сторон (xi, yi), то x1 + x2 + ... + xn = 0 и y1 + y2 + ... + yn = 0, поэтому общая сумма x1 + ... + xn + y1 + ... + yn должна быть четной! Но если сумма r1 + ... + rn нечетна, она также нечетна, и построить многоугольник невозможно.
, ... В некоторых случаях можно взять в качестве длин сторон первые n чисел, но в некоторых случаях этого сделать точно нельзя. Все зависит от четности. Если сумма r1 + r2 + ... + rn нечетна, это невозможно сделать. В самом деле, каждую сторону можно представить вектором (xi, yi), xi2 + yi2 = ri (xi и yi могут быть отрицательными). Если число ri четно, сумма xi + yi также четна. Если ri нечетно, то и xi + yi нечетно. Если можно построить многоугольник с векторами сторон (xi, yi), то x1 + x2 + ... + xn = 0 и y1 + y2 + ... + yn = 0, поэтому общая сумма x1 + ... + xn + y1 + ... + yn должна быть четной! Но если сумма r1 + ... + rn нечетна, она также нечетна, и построить многоугольник невозможно.
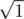 ,
, 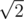 ,
, 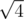 ,
, 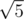 и т.д., т.е. корни целых чисел, представимых в виде a2 + b2. Сгенерируем достаточное количество таких чисел. Обозначим их
и т.д., т.е. корни целых чисел, представимых в виде a2 + b2. Сгенерируем достаточное количество таких чисел. Обозначим их 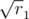 ,
, 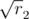 , ... В некоторых случаях можно взять в качестве длин сторон первые n чисел, но в некоторых случаях этого сделать точно нельзя. Все зависит от четности. Если сумма r1 + r2 + ... + rn нечетна, это невозможно сделать. В самом деле, каждую сторону можно представить вектором (xi, yi), xi2 + yi2 = ri (xi и yi могут быть отрицательными). Если число ri четно, сумма xi + yi также четна. Если ri нечетно, то и xi + yi нечетно. Если можно построить многоугольник с векторами сторон (xi, yi), то x1 + x2 + ... + xn = 0 и y1 + y2 + ... + yn = 0, поэтому общая сумма x1 + ... + xn + y1 + ... + yn должна быть четной! Но если сумма r1 + ... + rn нечетна, она также нечетна, и построить многоугольник невозможно.
, ... В некоторых случаях можно взять в качестве длин сторон первые n чисел, но в некоторых случаях этого сделать точно нельзя. Все зависит от четности. Если сумма r1 + r2 + ... + rn нечетна, это невозможно сделать. В самом деле, каждую сторону можно представить вектором (xi, yi), xi2 + yi2 = ri (xi и yi могут быть отрицательными). Если число ri четно, сумма xi + yi также четна. Если ri нечетно, то и xi + yi нечетно. Если можно построить многоугольник с векторами сторон (xi, yi), то x1 + x2 + ... + xn = 0 и y1 + y2 + ... + yn = 0, поэтому общая сумма x1 + ... + xn + y1 + ... + yn должна быть четной! Но если сумма r1 + ... + rn нечетна, она также нечетна, и построить многоугольник невозможно.Возьмем числа r1, ..., rn, если их сумма четна, иначе возьмем r1, ..., rn + 1 и выбросим одно из них, чтобы сделать сумму четной (в своем решении я выбрасываю наибольшее из таких чисел). Для каждого ri выберем неотрицательные xi и yi, xi2 + yi2 = ri. В общем случае существует 8 возможных ориентаций вектора (xi, yi), ( - xi, yi), (xi, - yi), ( - xi, - yi), (yi, xi), ( - yi, xi), (yi, - xi), ( - yi, - xi). Решим следующую подзадачу - заориентировать векторы таким образом, чтобы их сумма равнялась нулю. Это можно сделать при помощи следующего жадного алгоритма. Будем перебирать векторы, начиная с наибольших по длине. Будем вычислять текущую векторную сумму, которая изначально равна (0, 0) и будет пересчитываться при каждом добавлении вектора. На каждом шаге будем выбирать ориентацию, минимизирующую текущую сумму (по длине) при добавлении к ней. Затем, когда векторы заориентированы, отсортируем их по полярному углу и, прибавляя их последовательно, получим выпуклый многоугольник. Описанный алгоритм находит требуемый многоугольник на всех возможных тестах.









 0
0

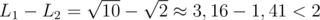 .
.

