357A - Кружок школьников
В задаче нужно было перебрать все варианты проходного балла от 1 до 100 и для каждого варианта посчитать, какие получаются размеры групп. Если нашли подходящие разбиения, выводим соответствующий одном из них проходной балл, иначе выводим 0.
357B - День Флага
Будем обрабатывать танцы в порядке их исполнения, и определять цвета формы участвующим в них танцорам. Если в текущем танце нет ни одного ранее танцевавшего участника, то назначим всем троим танцорам различные цвета формы произвольным образом. В случае же, если есть один такой танцор, тогда для него цвет формы уже известен. Два других цвета формы произвольным образом распределим между остальными двумя танцорами.
356A - Рыцарский турнир
Пусть в очередной битве (l, r, x) сражается K рыцарей. Тогда в этой задаче было достаточно научиться находить всех этих рыцарей за время O(K) или O(KlogN). Рассмотрим несколько способов сделать это.
Способ первый: хранить множество рыцарей в std::set (C++) или в TreeSet(Java). Тогда в C++ мы можем использовать метод lower_bound для нахождения самого первого живого рыцаря в отрезке, а потом итерироваться по множеству, переходя каждый раз к следующему по номеру живому рыцарю. В Java мы бы для этих целей использовали метод subSet.
set<int> alive;
for (int i = 0; i < n; i++)
alive.insert(i);
for (int i = 0; i < m; i++) {
int l, r, x;
scanf("%d%d%d", &l, &r, &x);
l--, r--, x--;
set<int>::iterator it = alive.lower_bound(l);
vector<int> toErase;
while(it != alive.end()){
int cur = *it;
if(cur > r)
break;
if(cur != x){
toErase.pb(cur); answer[cur] = x;
}
it++;
}
for (size_t j = 0; j < toErase.size(); j++)
alive.erase(toErase[j]);
}
Способ второй: определим массив next, значения в котором будут иметь следующий смысл:
- если рыцарь v живой, то next[v] = v;
- если рыцарь v выбыл, то next[v] указывает на некоторого рыцаря u > v (next[v] = u), такого, что между v и u нет живых рыцарей.
Тогда для того, чтобы для рыцаря v найти следующего по номеру живого рыцаря, нужно пройти по ссылкам next до первого живого рыцаря. Чтобы не ходить многократно по одним и тем же ссылкам, применяем эвристику сжатия путей из DSU. Надо учитывать случай, когда текущий рыцарь последний и уже выбыл из турнира.
int getNext(int v){
if(next[v] == v)
return v;
return next[v] = getNext(next[v]);
}
...
int cur = getNext(l);
while(cur <= r){
if(cur == x){
cur = cur + 1;
}else{
answer[cur] = x;
next[cur] = cur + 1;
}
cur = getNext(cur);
}
356B - Ксюша и Хемминг
Обозначим первую строку за x, |x| = lenX, вторую строку за y, |y| = lenY. Пусть L=НОК(lenX, lenY). Очевидно, что для тех больших строк a и b, которые описаны в условии, L является периодом, поэтому достаточно решить задачу для длины L, а затем умножить ответ на 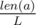 . Зафиксируем позицию i в строке x и посмотрим, с символами в каких позициях в строке y будет сравниваться символ xi. Из несложных соображений теории чисел это будут такие позиции 0 ≤ j < lenY, что i ≡ j (mod g), где g=НОД(lenX, lenY). Для каждого возможного остатка r от деления на g и каждого символа c можно посчитать count(r, c) — количество символов c, которые встречаются в y на позициях j таких, что j mod g = r. Тогда при вычислении расстояния Хэмминга напротив символа xi будет ровно count(i mod g, xi) таких же символов, а все остальные сравнения прибавят единицу к расстоянию Хэмминга.
. Зафиксируем позицию i в строке x и посмотрим, с символами в каких позициях в строке y будет сравниваться символ xi. Из несложных соображений теории чисел это будут такие позиции 0 ≤ j < lenY, что i ≡ j (mod g), где g=НОД(lenX, lenY). Для каждого возможного остатка r от деления на g и каждого символа c можно посчитать count(r, c) — количество символов c, которые встречаются в y на позициях j таких, что j mod g = r. Тогда при вычислении расстояния Хэмминга напротив символа xi будет ровно count(i mod g, xi) таких же символов, а все остальные сравнения прибавят единицу к расстоянию Хэмминга.
private void solve() {
Scanner in = new Scanner(System.in);
long n = in.nextLong(), m = in.nextLong();
String x = in.next(), y = in.next();
int lenX = x.length(), lenY = y.length();
int g = gcd(lenX, lenY);
long L = lenX * (long)lenY / g;
long answer = L;
int[][] count = new int[g][26];
for (int j = 0; j < lenY; j++) {
count[j % g][y.charAt(j) - 'a']++;
}
for (int i = 0; i < lenX; i++) {
answer -= count[i % g][x.charAt(i) - 'a'];
}
System.out.println(answer * (n * lenX / L));
}
356C - Купе
В данной задаче требовалось придумать какой-нибудь правильный жадный алгоритм. Один из правильных подходов делает следующее:
- Сначала соединяет все <<двойки>> с <<единичками>> (образуются <<тройки>>), путем пересаживания <<единичек>>.
- Рассматривает два случая в зависимости от того, <<единичек>> больше изначально или <<двоек>>. Если больше единичек, то пробует соединять оставшиеся после первого пункта одинокие <<единички>> в тройки, если <<двоек>>, то пробует из каждых трех <<двоек>> образовать две <<тройки>>.
- После применения пункта два, могут остаться еще какие-то <<единички>> или <<двойки>>. Нужно разобрать случаи того, что осталось, руками (случаев будет мало).
В задаче нужно руководствоваться скорее здравым смыслом, нежели какими-то известными жадными соображениями. Неплохо помогает написать стресс-тестирование с наивным решением (обходом в ширину), чтобы убедиться в корректности вашей жадности.
356D - Монеты и мешочки
Очевидно, что мешки и отношения "лежит непосредственно в" образуют лес. К каждой вершиной должно быть связано некоторое число ci — количество монет в соответствующем мешке. Тогда, если мы для каждой вершины посчитаем величину fi — сумма значений cj в поддереве этой вершины, то должны выполняться следующие условия:
- fi = ai
- сумма fi по вершинам, которые являются корнями деревьев, равна s.
Очевидно, что мешок с наибольшим ai будет корнем какого-то из деревьев. Также достаточно легко понять, что решение задачи существует тогда и только тогда, когда можно выбрать такой набор ai1, ai2, ..., aik, что сумма ai1 + ai2 + ... + aik равна s, причем один из мешков с наибольшим ai входит в такой набор. В одну сторону это очевидно, в другую покажем конструктивно: пусть у нас есть такой набор. Тогда все мешки, вошедшие в набор, кроме самого большого, будут "отдельными", то для них ci = ai, а все не вошедшие мешки мы последовательно положим друг в друга и в первый, получив матрешку (т.е. дерево с корнем в самом большом мешке будет ориентированной цепью).
Задача свелась к задаче о наборе суммы s из предметов a1, ... an. Это задача является NP-полной, и обычно в подобных ограничениях решается так: пусть T(i, j) = 1, если можно набрать сумму j, используя какие-то из первых i предметов, и T(i, j) = 0 в противном случае. Тогда 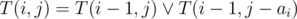 . Заметим, что i-ая строка этой таблицы зависит только от (i - 1)-ой, поэтому можно хранить в памяти не всю таблицу, а только две строки. Дальше мы будем использовать то, что значения в таблицы — это нули и единицы, поэтому мы можем хранить строчки таблицы побитово, в массиве из 4-битных целых чисел. Тогда, чтобы получить очередную строчку, мы должны сделать побитовое ИЛИ предыдущей строки и предыдущей строки, сдвинутой на ai бит. Все это можно сделать за
. Заметим, что i-ая строка этой таблицы зависит только от (i - 1)-ой, поэтому можно хранить в памяти не всю таблицу, а только две строки. Дальше мы будем использовать то, что значения в таблицы — это нули и единицы, поэтому мы можем хранить строчки таблицы побитово, в массиве из 4-битных целых чисел. Тогда, чтобы получить очередную строчку, мы должны сделать побитовое ИЛИ предыдущей строки и предыдущей строки, сдвинутой на ai бит. Все это можно сделать за 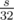 действий, поэтому выяснить, можно ли набрать сумму s, можно примерно за
действий, поэтому выяснить, можно ли набрать сумму s, можно примерно за 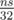 операций. Однако, тут нужно применить один трюк для того, чтобы восстановить, какие именно предметы нужно взять. Давайте для каждого значения суммы j будем запоминать величину first(j) — номер такого предмета, после рассмотрения которого стало возможно набрать сумму j. Это позволит нам восстановить ответ.
операций. Однако, тут нужно применить один трюк для того, чтобы восстановить, какие именно предметы нужно взять. Давайте для каждого значения суммы j будем запоминать величину first(j) — номер такого предмета, после рассмотрения которого стало возможно набрать сумму j. Это позволит нам восстановить ответ.
356E - Ксюша и строковая задача
Во время контеста большинство участников писали решение задачи очень похожее на авторское. Одно из авторских решений (более простое) использует полиномиальные хеши (хотя есть решения и без них). Кратко опишем решение.
Для каждой позиции i посчитаем с помощью хешей максимальное такое Li, что подстрока s[(i - Li + 1)..(i + Li - 1)] является строкой Грея. Так же посчитаем максимальное такое Pi, что подстрока s[(i - Pi + 1)..(i + Pi - 1)] отличается от строки грея не более чем на один символ. Очевидно, что Pi ≥ Li. Причем если Pi > Li, то также сохраним позицию символа и символ, который различает подстроку и некоторую строку Грея.
Понятно, что если бы не нужно было менять символы, тогда ответ был бы равен
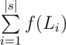 , где f(L) = 12 + 32 + 72 + ... + L2. Посчитаем ответ, без замены символов.
, где f(L) = 12 + 32 + 72 + ... + L2. Посчитаем ответ, без замены символов.Теперь переберем позицию и новый символ, на который будем менять символ в данной позиции. Как понять, на сколько поменяется ответ на задачу? Посмотрим на все строки грея, вхождения которых перекрывают зафиксированную позицию. После изменения символа на другой, они все перестанут быть строками грея (вычтем их длину в квадрате из ответа). Посмотрим на все строки Грея, которые отличаются ровно в одной зафиксированном символе от некоторой подстроки строки. После изменения на этот символ они все добавятся в ответ (их длину в квадрате нужно добавить в ответ).
Суммируя вышесказанное, с помощью Pi Li нужно, используя update на отрезке в offline, посчитать для каждой позиции и символа, на сколько поменяется ответ на задачу, если в данной позиции поставить этот символ. Далее нужно обновит ответ всеми возможными значениями.











Hi, would you please help me to clarify the problem 356B — Xenia and Hamming " It it easy to conclude that it will be compared with such yj that i ≡ j (mod g), where g = GCD(lenX, lenY)."
How to get that conclude?
Thanks
let's say ith character in the kth repetition of x is matched with jth character in the pth repetition of y
(k * x + i) mod gcd = i mod gcd (p * y + j) mod gcd = j mod gcd
I still can't get it. How do we conclude the gcd part? Would someone explain it in more details, please?
Let us consider the ith character in the xth repetition of the first string. And let us assume that it is matched with the jth character of the yth repetition of the second string. Then - (x*Len1+i) = (y*Len2+j) Should be true. Where Len1 and Len2 are the lengths of the first and second strings respectively.
If g = gcd(Len1,Len2), then we can write the equation as - (x*Len1+i) %g = (y*Len2+j) %g Hence, we get- i%g = j%g
For DivI A, I think it is more convenient to use the
erasemethod inset:I had a different solution for Div 1 C, which I think is easier to prove to yourself and harder to miss a case in.
Let's sort the numbers. Then, intuitively, it seems that there should exist a border in sorted train which splits the carriages into two parts — carriages with no students in it [first part], and carriages with 3 or 4 students in it [second part] (I would be very glad if someone could give me general proof for that [if more people were allowed in carriages and not just four] — maybe this isn't true in general case).
So let's check all possible border locations. Now that we have it fixed, let's denote four values, which can be computed in O(1) using partial sums:
Now, source <= free should hold, otherwise this scenario is impossible.
If source >= target (aka, transferring all students from first part to second will do), then we mark source as a potential answer.
Otherwise, we have to use students from second carriage, so if additional >= (target-source), then we mark target as a potential answer.
These are all the cases we have to worry about and the total complexity is O(N log N) or O(N) if you're bothered with doing count sort.
The proof for the first statement. It is clear that we don't need to empty any carriage with more than 3 students. Also, emptying a carriage with 2 students and filling a carriage with 1 student is not optimal, since it is better to put that 1 student in the carraige with 2 guys. Thus there is such a border, and it is somewhere before the first carriage with more than 2 guys.
UPD: sorry, I misunderstood, it's only a proof for a maximum of 4 people in carriage.
Okay, the proof for the general statement is essentially the same. Suppose we empty a carriage with b people and fill a carriage with a people, a < b. It is clear that we better empty the carriage with a people, hence contradiction.
А как же ситуация в задачи B, когда есть 2 и более участников с известными цветами и цвета их схожи?
Согласно условию, в каждом танце участвует максимум один танцор, который танцевал ранее.
по условию задачи этот танец перестает быть зрелищным
Would someone point out why I'm getting a wrong answer on test 26 for this submission 4808669 and 4799577 on 356B - Ксюша и Хемминг
Are you sure you are using 64-bit integers? (like long long)
yes, I used
unsigned long longIn Problem "356D — Bags and Coins" , can we write masks in unsigned long long , so we can solve the problem in n*s/64 operations ?
But you should keep in mind that oprations on long long are slower than operations on int
Yes , I know time will be the same , but those bitmasks was needed on opencup contest , where 64 bits didn't passed (WA) , 32 passed , so I am asking what is wrong with 64 bit integers .
Математическое решение C, для тех, кто не любит магические жадности. =)
Пускай изначально ai — количество купе с ровно i школьниками (на купе без школьников забьем). Сначала добавим в какие-то купе некоторое количество школьников, а потом попробуем удалить то же количество, чтобы выполнились условия.
Пусть мы bi раз добавили школьника в купе, где непосредственно перед этим было i школьников. Тогда b1 ≤ a1, b2 ≤ a2 + b1, b3 ≤ a3 + b2.
Теперь будем удалять. Мы обязаны удалить всех школьников из купе с 1 и 2 школьниками и можем удалить по одному школьнику из 4. Поэтому должно выполняться неравенство (a1 - b1) + 2(a2 + b1 - b2) ≤ b1 + b2 + b3 ≤ (a1 - b1) + 2(a2 + b1 - b2) + a4 + b3. Преобразуем: a1 + 2a2 ≤ 3b2 + b3, 3b2 ≤ a1 + 2a2 + a4.
Переберем b2. Из неравенств (и здравого смысла) получаем, что max(b2 - a2, 0) ≤ b1 ≤ a1, max(a1 + 2a2 - 3b2, 0) ≤ b3 ≤ a3 + b2. Ответ равен b1 + b2 + b3, поэтому b1 и b3 выгодно брать равными соответствующей нижней границе, при этом неравенства не должны быть противоречивыми.
There is a typo for problem E: f(L) = 12 + 33 ...
В DIV1A можно также использовать Segment Tree с покраской на отрезке: обойти раунды с конца, окрашивая интервалы [l, x) и (x, r] в x.
Можно, но уж точно не нужно.
Решение с set-ом очень короткое и быстро пишется (сдавали его уже на 4-ой минуте). Обвеска к дереву отрезков занимает не меньше строк кода, а ведь нужно еще написать или скопипастить само дерево...
В раунде не участвовал, но после того, как увидел задачу, написал правильное решение примерно за 10 минут (дерево было pre-written). Согласен, что дерево — это не то, что хотели увидеть авторы, но на войне все средства хороши, если правила не нарушают.
Am I the only one who thinks that Compartments was an ugly problem? I got the wrong the wrong idea and I had to deal with eleven or thirteen cases and of course I had holes in my solution, but even when got the good idea this wasn't a nice problem. And editorial for this task is the best proof.
I'm not fond of it, but it's not really that bad. There is a solution in which you don't have any cases or choices to make. If you try to fix the number of compartments in the final solution, the number of 3-compartments and 4-compartments is uniquely determined. Looking at the input and the fixed candidate solution in sorted order you may have something like:
Say you fix the number of compartments to 5.
1 2 2 3 4 4
0 3 3 3 3 4
You just add the absolute difference for each position and then divide by 2. You can do that efficiently by using frequencies instead of values in about 3 — 4 lines of code.
It's the kind of problem that teaches you to keep things simple (don't assume anything, jut try everything) which is a welcome reminder from time to time.
Yes, I know that solution (marcin_smu told me that) and I think that this is the nicest one. Indeed, I fell in trap of thinking "this can be done in any way!" and choose the wrong one, but as you can see, even author of this problem wasn't aware of that solution without any case-analysis.
Wrong tutorial? 357 B -FLAG DAY What if this is the test case n=6 m=3 dance1 1 2 3 dance2 1 4 5 dance3 4 2 6
the algorithm could fail on it.
Please, read the statement carefully before asking such questions. This case is not valid because in dance 3 we have two dancers (2 and 4), who had participated in some of the previous dances.
I am sorry, didnt get the problem statement. Now its clear. Thanks
Задача: 356D — Монеты и мешочки
"Давайте для каждого значения суммы j будем запоминать величину first(j) — номер такого предмета, после рассмотрения которого стало возможно набрать сумму j."
а как вы быстро находили суммы появившиеся после рассмотрения данного элемента? вам же нужно это сделать скорей чем за s (например за s/32)
Пусть у нас есть битсет x сумм, которых мы можем набрать используя первые i-1 предметов. Тогда при добавлении I-го предмета мы перейдем в битсет y = x | x << a[i]. Рассмотрит x XOR y. Он будет содержать единицы в ьитах, соответствующих тем суммах, для которых first как раз равен I. теперь необходимо проитерироваться только по единичным битам этого битсета, что можно сделать за быстро.
Не мог бы ты объяснить как быстро итерироваться по 1 в битсете? Там можно как-то брать по 32 бита и проверять равны лы они 0?
Насколько я знаю на C++ придется написать свой битсет для этого.
У std::bitset в libstdc++ (GCC) есть методы _Find_first() -> first_index и _Find_next(prev_index) -> next_index. Полное решение: 4830622.
Поясните пожалуйста задачу 356B — Ксюша и Хемминг.
"Несложные соображения из теории чисел"? Можно ли чуть более развернуто это написать? Непонятно, почему это правда.
In the second solution for Knight Tournament, if we set "next[cur] = cur + 1;", my understanding is we would always end up traversing each element, though we would process only the ones which are alive. Instead I think we should do
next[cur] = getNext(cur + 1); cur = next[cur];
Is my understanding correct or am I missing something here ?
magic happens in getNext function :)
Есть ещё одно, чисто программистское решение задачи 356C - Купе — для тех, кто не любит магические жадности и писать формулы.
Пусть у нас всего s школьников. Тогда нам надо сотворить f купе по 4 человека и t купе по 3 человека, причём так, что 4f + 3t = s. Рассмотрим произвольные такие t и f. Надо каким-то образом определить, какие из купе будут тройками, какие — четвёрками, а какие — нулями (имеется в виду количество школьников в них). Понятно, что, чтобы минимизировать количество пересаживаний, надо выбрать f купе с максимальным количеством школьников и сделать их четвёрками. Из остальных купе выбрать t максимальных и сделать их тройками.
Отсюда получается решение. Отсортируем массив a по убыванию. Найдём максимальное возможное f и запишем в массив b сначала f четвёрок, потом t троек, а всё остальное заполним нулями. Найдём сумму всех несоответствий по всем купе (это будет удвоенное количество школьников, которых надо переместить). Все остальные пары f и t мы можем получить, уменьшая f на 3 и увеличивая при этом t на 4. При каждом таком изменении массив b изменяется только в четырёх местах: последние 3 четвёрки заменяются на тройки, и первый 0 заменяется на 3. Каждый раз нам надо O(1) операций, чтобы пересчитать сумму всех несоответствий. Получается решение за O(n).
Вот реализация: 6475915.
I'm trying to solve prob.A with dsu, also used path compression. Even though all test cases must use same amount of mem for my code, got MLE for 22nd case although n=100 http://ideone.com/MUWaHY
My solution for div1 A gives TLE, but approach is same as given in editorial. Any idea why? Iam simply deleting elemnts in each match, so the worst case complexity is O(n*log^2(n)), when each match has only 2 knights because code
It's long time! Do you understand now, what was the problem ? I face same problem Here is my code : CODE
How to solve Div1A (Knight Tournament) using Lazy Propagation on Segment Tree. I am unable to build up the concept how to make Segment Tree and how to handle it for queries. Can anybody help me please?
hello , i just finished that problem ,
create a segment tree where you keep in each node the number of killed knight in that interval
and each time you get a query ,divide that interval into 2 intervals ( to ignore the alive knight )
and execute an update on the tree , PS( i didn't use lazy propagation technique )
you can see my code here and ask me any question , submission
I had finished the problem too, actually I was learning the lazy Propagation concept in segment tree. So, I was trying to solve this problem by Lazy Propagation. However, problem can be solved without using Lazy Propagation too.
i think that sometimes your update function works in O(N)
In the seg tree he is not doing point update instead doing range update but as the range of update is decreasing so it works.
can u explain more ?
it seems like it will give TLE
Hi, So my method is the same as the one in the editorial,I used std::set but I cant figure out why my solution is getting TLE,please help.. 28733152
Faced the same problem. Have a look to this: http://codeforces.net/blog/entry/19043
Knight Tournament also solvable with ST (each node is true if there's any alive leaf, false otherwise)
Can you explain how to solved Knight Problem Use Segment tree please?,it will really helpful. Thanks in advance
Each knight is a leaf in the segment tree. Also, every leaf has the state 'true' if he's alive ('false' otherwise). A node in the segment tree has state 'true' if there's at least one knight alive in that sub-tree. So, every query kills all the knights in the given range, assigns the id of the killer knight accordingly, and also updates the states of every node. This state-updating thing is to avoid traversing dead ranges with no alive knight. Hopefully, it's clearer now how to use ST here :)
That means here we need two arrays, one to store the states and the other to store the IDs ,right?
Exactly
Thank you so much. This was very helpful.
there is some problem with the judge MikeMirzayanov Nerevar https://codeforces.net/contest/356/submission/80592110 https://codeforces.net/contest/356/submission/80592719 both of these are same but only 1 got AC