1) В силу небольших ограничений в задаче можно в цикле перебирать значения n и проверять условие 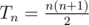
2) Определим граф, где буквы A, B, C - вершины, и если выполняется x < y, то существует ребро y - > x. Далее проведем топологическую сортировку. Если при выборе следующей вершины при поиске мы можем перейти в помеченную, но не использованную вершину, значит найден цикл, и надо вывести "Impossible".
3) Задача решается переборо 6! = 720 перестановок. Для каждой перестановки первые 3 слова будем располагать горизонтально, остальные - вертикально. Будем располагать слова так:
Для того, чтобы существовало решение, необходимы следующие условия:
Замечание: В C++ если хранить доску в виде vector<vector<char> > или vector<string>, то для обновления ответа можно просто использовать оператор "<".
4) Рассмотрим не самый эффективный алгоритм, тем не менее проходящий по времени, со сложностью O(mCn5log(Cn5)).
Рассмотрим 1 ответ системы: <number, v>. Общее число вариантов шифра будет Cnv - не очень большое число, поэтому можно их просто сгенерировать. Объявляем это множество вариантов текущим. Далее, для каждого нового ответа генерируем множество возможных шифров, пересечение текущего и нового множеств объявляем текущим.
В итоге получаем некое множество. Надо исключить из него элементы, которые уже были в ответах системы, и вывести его размер.
PS: В комментариях приветствуются более эффективные алгоритмы
5) Приведу пример решения за O((n + m)log(n + m)).
Предварительно исключим из рассмотрения стенки до которых снаряд не может долететь ни при каких условиях: x > v2 / g
В силу условия α < =π / 4 выполняется следующее
Отсортируем стенки по координате x. Теперь задача свелась к следующей: для каждого выстрела определить минимальный индекс стенки, при этом угол выстрела лежит между углами атаки стенки. А эту задачу можно решать деревом отрезков для минимума с возможностью обновления на интервале. Вначале заполним дерево значением KInf. Далее, для каждой стенки будем делать update(α1, α2, index). Потом пройдемся по запросам. Если getMin(α) == KInf, значит снаряд благополучно приземлится на землю, иначе врежется в стенку с индексом getMin(α).
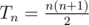
for (int n = 1; n <= Tn; n++)
{
if (n * (n + 1) / 2 == Tn)
{
cout << "YES\n";
return;
}
}
cout << "NO\n";
2) Определим граф, где буквы A, B, C - вершины, и если выполняется x < y, то существует ребро y - > x. Далее проведем топологическую сортировку. Если при выборе следующей вершины при поиске мы можем перейти в помеченную, но не использованную вершину, значит найден цикл, и надо вывести "Impossible".
3) Задача решается переборо 6! = 720 перестановок. Для каждой перестановки первые 3 слова будем располагать горизонтально, остальные - вертикально. Будем располагать слова так:
- hor[0], ver[0] - влево-вверх
- hor[2], ver[2] - вправо-вниз
- hor[1]: (len(ver[0]) - 1, 0)
- ver[1]: (0, len(hor[0]) - 1)
Для того, чтобы существовало решение, необходимы следующие условия:
- len(hor[0]) + len(hor[2]) == M + 1 // углы восьмерки
- len(ver[0]) + len(ver[2]) == N + 1 // углы восьмерки
- len(hor[0]) >= 3 && len(hor[2]) >= 3 && len(ver[0]) >= 3 && len(ver[2]) >= 3 // восьмерка невырождена
- буквы на началах/концах соответствующих строк совпадают
- совпадают буквы при пересечении hor[1], ver[1]
Замечание: В C++ если хранить доску в виде vector<vector<char> > или vector<string>, то для обновления ответа можно просто использовать оператор "<".
4) Рассмотрим не самый эффективный алгоритм, тем не менее проходящий по времени, со сложностью O(mCn5log(Cn5)).
Рассмотрим 1 ответ системы: <number, v>. Общее число вариантов шифра будет Cnv - не очень большое число, поэтому можно их просто сгенерировать. Объявляем это множество вариантов текущим. Далее, для каждого нового ответа генерируем множество возможных шифров, пересечение текущего и нового множеств объявляем текущим.
В итоге получаем некое множество. Надо исключить из него элементы, которые уже были в ответах системы, и вывести его размер.
PS: В комментариях приветствуются более эффективные алгоритмы
5) Приведу пример решения за O((n + m)log(n + m)).
Предварительно исключим из рассмотрения стенки до которых снаряд не может долететь ни при каких условиях: x > v2 / g
В силу условия α < =π / 4 выполняется следующее
- Функция дальности полета от угла монотонная
- Функция высоты при фиксированной дальности от угла монотонная
Отсортируем стенки по координате x. Теперь задача свелась к следующей: для каждого выстрела определить минимальный индекс стенки, при этом угол выстрела лежит между углами атаки стенки. А эту задачу можно решать деревом отрезков для минимума с возможностью обновления на интервале. Вначале заполним дерево значением KInf. Далее, для каждой стенки будем делать update(α1, α2, index). Потом пройдемся по запросам. Если getMin(α) == KInf, значит снаряд благополучно приземлится на землю, иначе врежется в стенку с индексом getMin(α).











Альтернативное решение задачи D.
Воспользуемся методом деления пополам.
Будем перебирать все возможные маски длины n/2. Предположим, что зафиксированная маска является первой половиной пароля не противоречащего входным данным. Для каждой такой маски будем формировать вектор (далее вектор А), в котором i-й элемент равен количеству совпадений первой половины i-ого введенного пароля и нашей зафиксированой маски. Для каждого такого вектора посчитаем сколько он встречается, для этог оможно использовать map.
Аналогичным образом перебираем и вторую часть, формируя при этом вектор совпадений (далее вектор B) для второй части паролей и зафиксированой маски.
Обозначим вектором S вектор ответов системы на введенные пароли. Тогда перебирая вторую половиу пароля у нас будет столько возможных паролей имеющих такую же вторую половину, как и наша маска, и не противоречащих условию, сколько у нас сужествует векторов А равных S-B.
Асимптотика этого решения равна O(2^(n/2)*m*n). Используя хэш мапу можно добиться асимптотики O(2^(n/2)*m) . Хочу заметить, что это решение не зависит от ограничения на количество верных цифр в введенных Васей паролях.
Я когда прочитал на контесте решил действовать в лоб. Ну и наркоманский код у меня получился, но получил AC и написал относительно быстро его(~ 20 минут)
http://codepad.org/H026teJ3
I did some pretty hardcore implementation in Div2B "so called proper brute force" can't be more brute have a look 60172369
We can see this problem as a directed graph, so we have to ensure that the following condition should be veryified to have an answer:
1. Every node in the graph should have not one degree at the same time.
2. There are no bidirectional edges.
With the first condition we ensure that there isn't a cycle, with the second we don't have a contradiction.
My sub: 60185706