| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 165 |
| 2 | maomao90 | 164 |
| 3 | Um_nik | 163 |
| 4 | atcoder_official | 160 |
| 4 | adamant | 160 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 8 | Dominater069 | 154 |
| 8 | nor | 154 |
Здравствуйте! Дан неориентированный граф. У меня возник вопрос:
Если есть вершины U и V и они в одной компоненте рёберной двусвязанности, а так же ребро E, которое так же в этой компоненте, то правда ли то, что есть путь, в котором ни одно ребро не встречается два раза, идущий из U в V и проходящий через ребро E?
Не очень понятно, что означает "вершина лежит в компоненте вершинной двусвязности", вообще говоря, компонента вершинной двусвязности — множество ребер.
Если вопрос про компоненту реберной двусвязности, то ответ да. Можно действовать так. Считаем, что эта компонента — весь граф. Пусть $$$A$$$ и $$$B$$$ — концы ребра $$$E$$$. Стянем это ребро. Граф, очевидно, останется двусвязным. Теперь рассмотрим некоторый цикл $$$C$$$, на котором лежат вершины $$$U$$$ и $$$V$$$. Проведем из вершины, соответствующей "склеенным" $$$A$$$ и $$$B$$$ два пути в $$$U$$$. Эти пути впервые пересекут цикл $$$C$$$ в точках $$$W_1$$$ и $$$W_2$$$. Тогда путь $$$U \to W_1 \to AB \to W_2 \to V$$$ искомый.
Наверное, можно вопрос понять как "пусть дан вершинно двусвязный граф, ...". Кажется, что тогда он и реберно двусвязный, из чего все следует.
извините, действительно перепутал реберную и вершинную((
а что значит "стянем" ребро? т.е. сделаем так, чтоб А и Б стали одной вершиной?
Да, удаляем вершины $$$A$$$ и $$$B$$$, а затем добавляем новую, в которую проводим все ребра, которые шли в $$$A$$$ или в $$$B$$$.
Большое спасибо! Понял ваше решение.
Кажется, Ваше доказательство неверно. Рассмотрим граф на картинке. Цикл $$$C$$$ выделен синим ($$$U - 1 - V - 2 - U$$$), два пути обозначены красным ($$$AB - U$$$ и $$$AB - 1 - U$$$). Тогда $$$W1 = U$$$, $$$W2 = 1$$$, и предложенный путь не проходит по ребру $$$A - B$$$.
Мне утверждение интуитивно кажется верным, но придумать доказательство, а особенно красивое-короткое, пока не получается.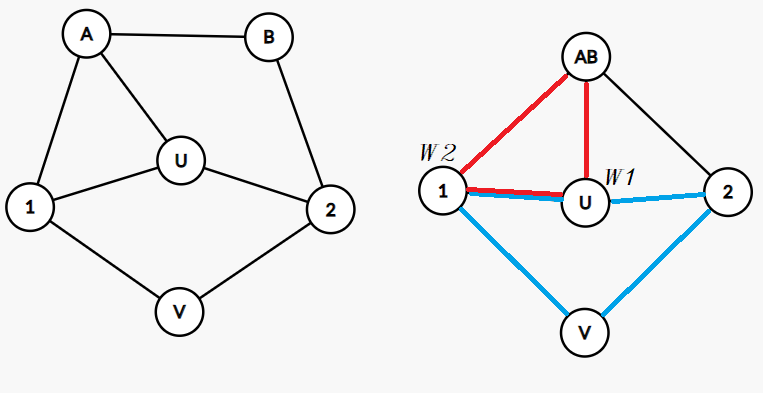
Да, действительно, прошу прощения. Вероятно, тогда пройдет трюк "поставим дополнительную вершину на ребро", но тут нужно доказывать, что граф останется двусвязным.
Так как граф двусвязный если и только если в нём нет мостов, то вроде это очевидно. Красивый трюк!
Да, действительно)