Обсуждаем задачи тут.
Я участвовал в Div.2.
И меня интересует, почему Дейкстра с сетом дает WA#16 в G.
И хэширование + дп + бин.поиск дает WA#2 в J.
Я уже просто запарился искать ошибку.
Я участвовал в Div.2.
И меня интересует, почему Дейкстра с сетом дает WA#16 в G.
И хэширование + дп + бин.поиск дает WA#2 в J.
Я уже просто запарился искать ошибку.
Интересует, как сдавать F с первой попытки))
И ещё, как в J обойти ограничение по памяти, если строить решение на хэшах (по моим подсчётам 8 * 10 000 * 10 000 / 2 как бы многовато, а писать хэши на 4 байта как-то стрёмно да и это тоже еле влезет).
В условии было сказано что суммарная длина всех текстов не превышает 10000, следовательно хэшировать строк нужно будет меньше, т.к. k2 можно ограничить как k2 = min(k2, n, m).
Мы находили для каждого суффикса второй строки наибольший его префикс, который встречается в первой. Для этого во внешнем цикле перебирали длину строки, а во нутренних формировали хэшмаму с подстроками из первой строки зафиксированной длины и релаксировали длины префиксев суфиксов.
После этого был оквадратичное ДП, которое можно было свести к n*log(n) RMQ.
Формирование наибольших префиксов суффиксов содержащихся в 1й строке у нас занимало чуть больше секунды, квадртичное ДП работало примерно за такое же время => наша команда отхватывала TL. Предположительно дп за н лог н решило бы проблему, но было 5 минут до окнца контеста %)
ЗЫ Важным моментом было то что набо дыло уметь обнулять все массивы за О(1)
ЗЫ2 Данный пост не претендует на правильное решение %)
скорее всего по-нормальному J решается через какие-нить суффиксные автоматы или какой нибудь ахо-корасик.
5000 5000 1 5000
a x 5000
a x 5000
задача работает чуть меньше секунды (если собирать при помощи g++ -O -march=pentium4m, иначе работает секунды 3)
Код: http://pastie.org/1373220
итого решение за 10^7*26. нужно быть очень аккуратным с константой.
У нас прошло такое решение:
1) Перебираем первые четыре буквы слова - это 264 вариантов.
Вычисляем хеши от этих строк из 4-х букв.
Запоминаем для каждого хеша, как мы его получили.
2) Затем генерируем случайную строку из 25-35 символов, первые 4 символа которой делаем нулевыми.
Вычисляем от неё хеш и смотрим, сколько надо добавить, чтобы получить нужное значение.
Если такое число было среди заранее вычисленных хешей для первых четырёх символов, то ставим эти символы и выводим ответ, иначе генерируем новую случайную строчку.
Это решение, как мне кажется, можно ещё немного модифицировать: брать не первые четыре символа, а, например, 1-ый, 42-й, 99-й и 167-й (когда мы берём первые четыре, а основание p - маленькое, то будет много коллизий среди этих 264 хешей). И в случайной строчке несколько букв зафиксировать, а генерировать несколько как-то разбросанных по ней.
Количество перебираемых вначале букв тоже можно изменить.
В общем в итоге можно получить решение, которое работает в среднем за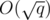
или около того.
хэш-таблица оно называется
http://ru.wikipedia.org/wiki/%D0%A5%D0%B5%D1%88-%D1%82%D0%B0%D0%B1%D0%BB%D0%B8%D1%86%D0%B0
Да, я понял свою ошибку. Я зациклился на том, что первая строка может быть ~10000, но не подумал, что такие длинные подстроки в этом случае уже не могут встречаться во второй строке. В общем в таком случае k2 = min(k2, длина второй строки) и проблема с памятью решается. А запихать хеши - это уже дело техники и кучи штрафов. Другого выбора не было, т.к. с z-функцией пока подружиться не довелось)
эх... если бы у нас тогда промелькнули в голове слова наподобие "z-функция" или "префикс-функция")) не страдали бы такой фигней в последний час
Ну мы вообще до реализации не дошли) Я лично планировал N^2 logN пихать, судя по отзывам это было наивно)))
Но вообще такую тему с хэш-таблицей на некоторых задачах с тимуса удавалось пропихнуть.
25 - это количество простых чисел меньше 100. как быстрее - непонятно. прекальк тоже в 64 Кб не лезет.
N превращается в
http://en.wikipedia.org/wiki/Partition_%28number_theory%29
http://en.wikipedia.org/wiki/Pentagonal_number_theorem
Задачи B и F не понравились :о)
Кто-нибудь знает/есть идеи как решать задачу D?
B прекрасно придумывается даже если не знать формулы (хотя про производящие функции мы знали, но думаю, это не очень секретное знание, подозреваю, что на математическом факультете любого вуза про них рассказывают). Тем более появляется дело для математика в команде, способное занять его на сколь-либо существенное время :)
Мне не нравится задача когда
а) Моих знаний до контеста не хватает, чтобы ее решить
и
б) После контеста, прочитав разбор, я не хочу пополнять эту дыру в знаниях.
Потому что такая задача не вписывается в мои субъективные представления о том, какие должны быть задачи на соревнованиях :о)
Ну не должен же быть весь контест из тупых задач с длинными решениями, красивая математика никогда не помешает.
Любители инвариантов могут посчитать что-то типа минимального возможного расстояния от блохи до собаки и заметить, что оно каждый ход уменьшается не более чем на 1.
Легко понять, что среди всех блох, которые могут добраться до собаки за минимальное время, есть хотя бы одна, которая может это сделать не прыгая (допустим, что это не так - тогда рассмотрим ту блоху, которая достигает собаку за минимальное время, и рассмотрим ее последний прыжок, после которого она идет не прыгая. очевидно, что та блоха, через которую она перепрыгнула, может за один ход встать на ту же клетку без прыжка, и продолжить движение по тому же марштуру после этого).
Ну а имея это знание просто ищем самую близкую блоху.
Уже почти неделю висит с Check failed, на clar никакого ответа.