| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
Только что закончилась Пятая командная олимпиада. Расскажите, пожалуйста, решение A и F. Мы с сокомандниками так и не смогли запихать B, в самом конце не успели исправить багу. Но у нас выходило очень много кода (примерно 500 строк). Расскажите как вы писали кратко эту задачу и можете, пожалуйста, код показать.
Также предлагаю здесь обсудить все остальные задачи.
В задаче В предполагалось довольно простое решение: заметим, что если мы можем походить как-то ладьей или слоном, то шаха от этого точно не будет. Поэтому, если мы можем так походить, походим туда-сюда и это будет верный двойной ход.
Если так походить нельзя, то надо ходить королем. Попытаемся походить во всех восьми направлениях и проверим, что не будет шаха. Если есть какой-то такой ход, то, опять же, походим туда-сюда и все будет хорошо. Если таких ходов нет, то -1.
P.S. Ладьей и слоном можно пробовать сдвигаться только на одну клетку, потому что понятно, что, если в верном двойном ходе мы сдвинулись какой-то фигурой больше, чем на одну клетку, то, если сдвинуть ее на одну клетку, хуже не будет.
Какой ответ на тест:
3 3
1 1 1 2 1 3
3 1 2 2 3 3
?
Тест некорректен — черному королю объявлен шах от белого слона.
Вроде никто никого не бьет: в частности, белый слон бьет только черную ладью, но не короля.
Надо внимательнее читать условие :)
"Королю объявляется шах, если есть такая фигура, которая будет бить короля после убирания с доски всех фигур кроме неё и короля."
То есть фигуры могут бить через другие фигуры.
У меня бы рука не поднялась так шахматы исковеркать.
Задача планировалась как легкая, поэтому и было сделано это изменение в шахматных правилах. Но ее все равно довольно плохо порешали :(
Обе интерактивки мы сдали полным рандомом.
В связи с этим, резонный вопрос: какие нормальные решения этих задач?
Ладно, если в той задаче, где надо ловить чувака в дереве, такие ограничения, что видно, что рандом наверняка зайдет ( ≤ 500000 переходов в ≤ 100 комнатах), то по другой явно существует норм решение.
Кто-нибудь поделится?
I: Мысленно подвесим дерево за вершину, где сидит чувак, которого мы ищем. Тогда нам надо прийти в корень. Поставим перед собой задачу — подняться в дереве вверх(т.е. уменьшить глубину). Пойдем по рандомному ребру, предварительно положив вершину в стек. Если теплее, то ок. Если холоднее, то решаем аналогичную задачу, но помним вершины в стеке, и каждый раз, когда поднимаемся, выбрасываем верхний элемент из стека. Теперь, когда мы пришли в лист, то мы точно поднимемся. Когда мы поднялись, то точно знаем в какой мы сейчас вершине (она хранилась в стеке), а значит знаем и по каким ребрам мы из нее уже ходили. Пойдем по очередному ребру (по которому еще не ходили). Таким образом мы так или иначе уменьшим глубину на 1 от изначальной (в худшем случае обойдя все поддерево). Потом повторяем этот процесс.
А можно взглянуть на Ваш код. Спасибо.
Пожалуйста
На самом деле там остались лишние вещи от предыдущего варианта решения. Понятно, что вектор Т не нужен, и что в массиве векторов Ж используется только размер векторов, так что сами элементы в нем не интересны.
Еще можно было сдать вот так. link
Это одно из преимуществ олимпиад по информатике, но лично я за красивые и строгие решения.
J: Подцепим все особые вершины, к 1ой особой ребрами веса 0. Нетрудно доказать, что сейчас путь в графе наименьший из всех возможных (доказывать от противного). Из того, как мы подцепили вершины следует, что наикратчайший путь проходит не более, чем через 2 особых ребра (ребро между особыми вершинами) и сначала идет какой-то префикс, потом особые ребра, а потом остаток пути. Переберем ребра, удаляя их, и смотря изменяется ли длинна кратчайшего пути (оставим ребра, от которых эта длинна зависит, т.е. через которые этот путь проходит). В конечном итоге у нас будет не более 2 особых ребер. Если ребра 2, то их можно заменить на 1. Получаем, что либо самый короткий путь не зависит от особых ребер, либо зависит от 1. Если не зависит, то проверяем и все. Если зависит, то мы можем получить длину в диапазоне [самый кратчайший путь; самый короткий путь без особых ребер], изменяя вес оставшегося ребра. Если наш диапазон и диапазон [l; r] пересекаются, то понятно, как посчитать новый вес ребра, если нет, то нет.
А как по-нормальному решалась H? Мы затолкали, добавив к перебору отсечение по времени.
Ну вот.. :(
Я решал так: Пройдем по всем вершинам. Для каждой будем пытаться добавить в номер бит, пройдя по всем 20 битам и увеличить значение в получившимся номере текущим значением. Потом еще раз пройдем, будем для каждого смотреть на номер с макс. кол-вом единиц и беря как ответ сумму штрих-кодов и ноомеров серий его и текущегою. Cложность 2 ^ n * n
A(i), B(i) — последовательности
dp(i) — макс. A(j) из всех A(i) где (i | j) == i
res(i) = B(i) + A(((1 << n) — 1) ^ i)
В B было принято решение быдлокодить, но даже с этим и моей большой шапкой получилось 190 строк кода.
Это тоже очень много, если что)
Ну там вывод можно сжать в одну функцию. Распихать фигуры в массив[3] и сжать ввод. Шапка 50 строк.
В авторском решении 120 строк, причём шапка тоже в 50 строк :)
Ну, и его можно укоротить, но такой цели не было.
Правда ли, что авторами подразумевалось решение задачи D за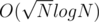
на запрос?
Да. Также можно решать за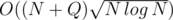
, выбрав размер блока порядка 
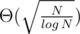(асимптотическое улучшение, да!)
Ой, вот вместо того, чтобы оценивать, надо ли загонять логарифм под корень или нет, проще, имхо, написать с произвольной константой K, которую потом подогнать на рандомных тестах или на сервере по фидбеку =) Там же перед каждым слагаемым из оптимизируемой нами суммы ещё какой-то коэффициент стоит.
Базовая номинация в Тренировках: 2013-2014 Цикл интернет-олимпиад. Пятая командная олимпиада, базовый уровень (10 ноября 2013 года).
И еще: 2013-2014 Цикл интернет-олимпиад. Пятая командная олимпиада, усложненный уровень (10 ноября 2013 года).
Я извиняюсь, но почему в тесте 81 тест m=102 ??? когда m<=n и n<=100 ? Из-за того что массив длины 100, не зашло это на олимпиаде ( и ответ выдавал WA на контесте, вместо ошибки исполнения, просто чудесно
А что за задача?
Последняя задача, интерактивка про отца Фёдора ( где надо кратч путь сделать заданной величины)
Вы же пишете на C++? Выход за границу массива в этом языке может вызывать что угодно. Если он мелкий, то скорее всего вы попадете в доступную вашей программе область памяти. Соотвественно при попытке прочитать прочитается какой-то бред, а при попытке записать запортится случайный кусок памяти, скорее всего начало другого массива. После этого понятно произойдет что угодно.
Но то что тест не удовлетворяет ограничениям остается ...
Скажите, почему не валили такое решение F:
Восстановим оптимальную расстановку : берем максимум из первого ряда и максимум из второго, соединим ребром(то есть эти стулья охраняет 1 человек). Этим ребром мы разделили на две половины, от каждой половины запустимся и сделаем тоже самое. Ответ — максимум из непроведённых рёбер(на контесте недопихалось, в дорешке заходит).
У этого решения проблемы, когда максимумов несколько.