I have had this doubt in dynamic programming for a long time now regarding which states to use. The question goes something like this:

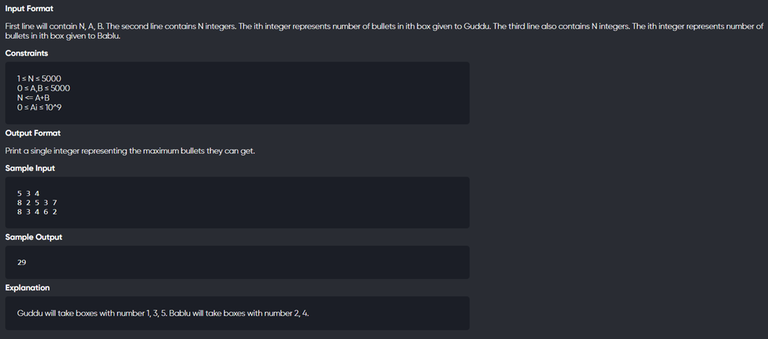
Reading Input:
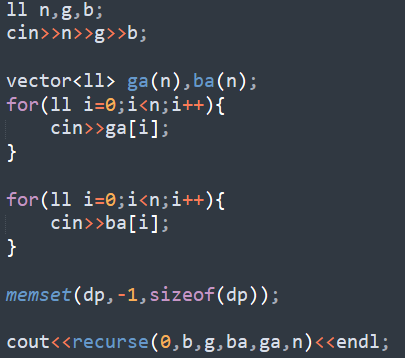
Recursion Code: So from the basic intuition I wrote this code. Which is obviously MLE: 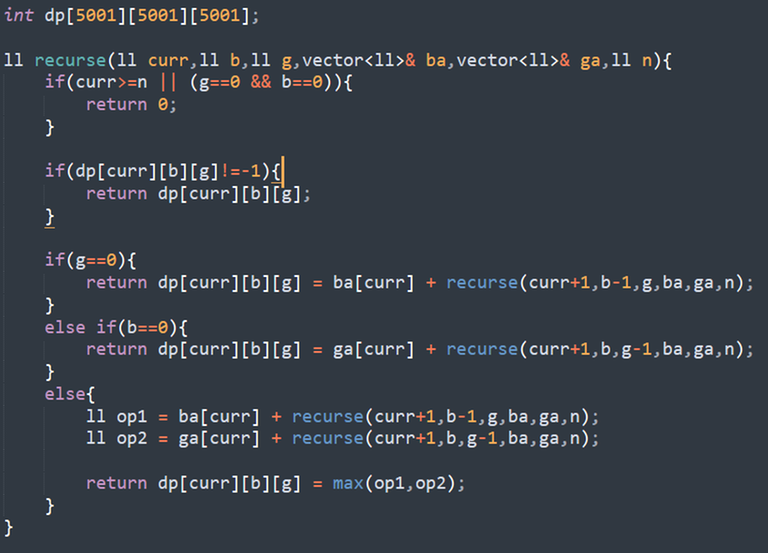
Then I tried this code: 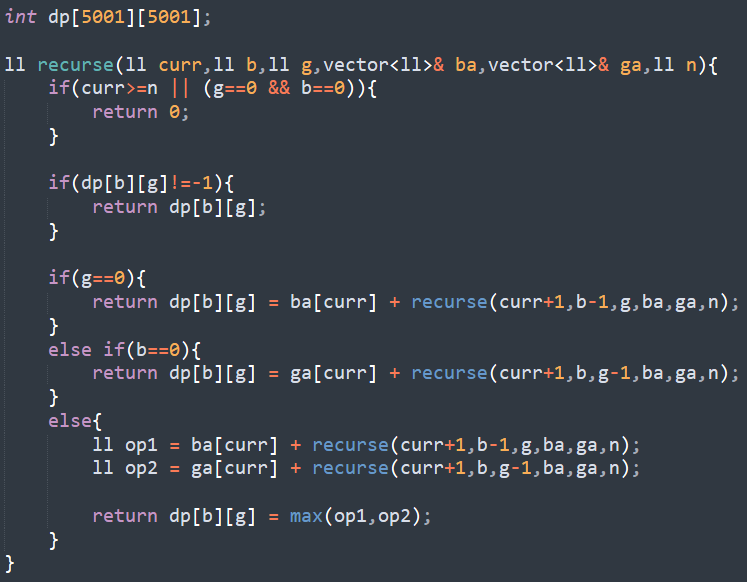
And this code passed the test cases and got AC. So now coming back to my doubt. There have been many problems where
$$$ dp[i][j][k] --> $$$ is optimized to $$$--> dp[i][j] $$$ because the state j is always changing. But I have also practiced questions where trying this $$$ dp[i][j][k] --> $$$ is optimized to this --> $$$ dp[i][j] $$$ and it got me a WA.
So can someone please explain when to take a state into consideration so that I dont fall into this MLE trap again in the near future?
Thank you:)











In your case, MLE was caused because you were allotting too much memory (5000*5000*5000*sizeof(int) bytes). In some other cases, MLE can be caused due to overflow during recursion (while performing recursive dp, probably).
But coming to states of a dp problem, it is a technique which can only be mastered by practice and practice only. There is no shortcut route in instantly understanding what should be the states for a particular dp problem. In general, you can sort of get an idea about the states from the constraints (say for a problem, where $$$N,M \le 2e5$$$, the intended solution obviously isn't $$$dp[N][M]$$$). This is something you can understand better by practising more and more problems on dp.
Any link for this problem
Problem link
I think your second code should have WA'd. Maybe you were lucky or can anyone convince me otherwise? To save memory in this case, it is enough to solve the problem in tabular style and use dp[2][a][b] then rollover dp values to represent the states as the transition only requires the previous dp array.
WA as in MLE or the logic is wrong?
not fully storing the states should WA. e.g
dp[i][j][k] should only be optimized to dp[i][j] if k is constant.
I believe this is so because dp[i][j][1] and dp[i][j][2] would be treated as the same state dp[i][j](when returning memoized value) which is wrong.
All I read was if a state is changing in every case you dont need to include it. Here curr+1 was happening in every transition. So we dont need to take it as a state.
All I read was if a state is changing in every case you dont need to include it.Source?
What if one of the recursive funtions had curr+2 instead, do you include curr or not?
What if your code only had one parameter which was curr. By your logic, you can optimize memory to O(1) i.e dp[1] then?
"What if one of the recursive funtions had curr+2 instead, do you include curr or not?" Then I would've included.
But curr is still changing in every case so you shouldnt include it going by your words. You included g as a parameter in dp array because g did not change in the recursive call after if(g==0) part right?
Before calling the recursive function, let $$$total$$$ = $$$b$$$ + $$$g$$$.
$$$curr$$$ in the current recursive step is uniquely determined by the $$$total$$$ — $$$b$$$ — $$$g$$$. So each $$$b$$$ and $$$g$$$ uniquely determine $$$curr$$$; Hence, there's no need to memorize $$$curr$$$. So, the $$$2nd$$$ solution is correct.
If there would've been a call like b+1,g or b,g+1 and also b-1,g and b,g-1. Then it would ve been important to keep the $$$curr$$$ right?
Not required, you can check this solution.
Here $$$dp[i][j]$$$ represent the maximum number of bullets we can take by using $$$i$$$ number of boxes from Guddu's set and $$$j$$$ number of boxes from Bablu's set.
And clearly it's recurrence relation is either we choose a box from Guddu's set or we can choose from Bablu's set
i.e. $$$dp[i][j]$$$ = max( $$$dp[i-1][j]+A[i+j-1]$$$ , $$$dp[i][j-1]+B[i+j-1]$$$ )
// we select from Guddu's set // we select from Bablu's set
Oh, didnt realize they could not skip any box number. I'm guessing if they could, memoizing curr is a must.