Разбор задач подготовили: Fefer_Ivan, NALP.
371A - K-периодичный массив
Для того, чтобы массив был периодическим, элементы 1, 1 + k, 1 + 2 * k, ... должны быть равны. Также, элементы 2, 2 + k, 2 + 2 * k, ... должны быть равны. И так далее до k. То есть существует k групп элементов, таких что каждый элемент принадлежит ровно одной группе. Каждая группа может рассматриваться независимо. Рассмотрим группу в которой a единичек и b двоек. Все элементы в одной группе должны быть равны. Для того, чтобы этого достичь необходимо либо все единички сделать двойками (что потребует a операций изменения), либо все двойки сделать единичками (что потребует b операций изменения). Для того, чтобы решение было оптимальным, необходимо выбрать способ, который требует наименьшее количество операций изменения.
371B - Как лисица сыр делила
Из условия понятно, что лисица может производить над числами лишь три операции: поделить какое-то из них на 2, поделить на 3 или поделить на 5. Для начала, давайте представим оба числа в форме a = x·2a2·3a3·5a5, b = y·2b2·3b3·5b5, где x и y не делятся ни на 2, ни на 3, ни на 5. Если x ≠ y, то понятно, что как бы лисица не делила числа a и b, то сравнять она их не сможет, а значит, следует вывести “-1”. В противном случае, требуется сравнять степени чисел 2, 3 и 5 в разложениях, за наименьшее количество операций это делается так: от наибольшей степени отнимается единица, пока она не сравняется с меньше степенью. Таким образом, ответ равен |a2 - b2| + |a3 - b3| + |a5 - b5|.
371C - Гамбургеры
Для решения этой задачи будем использовать идею бинарного поиска по ответу. Предположим, что ответ равен x, необходимо убедиться, что Поликарп сможет собрать именно столько гамбургеров и не потратит больше денег, чем у него есть. Давайте для x подсчитаем, сколько будет стоит собрать эти гамбургеры.
Пусть для одного гамбургера требуется сb кусочков хлеб, cs колбасы и cc сыра (эти данные нетрудно подсчитать из строки-рецепта “гамбургера от Поликарпа”). Тогда всего необходимо cb·x кусочков хлеба, cs·x колбасы и cс·x сыра. За лишние ингредиенты Поликарпу придется заплатить, поэтому в сумме он отдаст в магазине max(0, x·cb - nb)·pb + max(0, x·cs - ns)·ps + max(0, x·cc - nc)·pc рублей. Если это значение меньше, чем r, то Поликарп сможет сделать x гамбургеров, а иначе — нет.
С помощью бинарного поиска найдем такое максимальное x, что max(0, x·cb - nb)·pb + max(0, x·cs - ns)·ps + max(0, x·cc - nc)·pc ≤ r, такое число и будет ответом на задачу.
371D - Сосуды
Наивное решение этой задачи работает следующим образом. Давайте хранить количество жидкости в каждом сосуде в массиве v. Тогда для ответа на запрос второго типа надо просто взять значение из этого массива. Для выполнения запроса первого типа (налить x жидкости в сосуд i) надо выполнить следующую процедуру:
- Если x = 0 то вся вода уже использована, закончить процедуру.
- Если i > n то вся оставшаяся вода будет разлита на пол, закончить процедуру.
- Если x единиц воды помещаются в сосуд i, то прибавить x к v[i] и закончить процедуру.
- Заполнить сосуд i полностью и вычесть использованное для этого количество воды из x.
- Присвоить i = i + 1.
- Перейти к первому шагу.
В худшем случае, такая процедура будет итерироваться по всем сосудам для каждого запроса. Например, если у нас есть n сосудов вместимости 1, то запрос вида 11n потребует O(n) времени на выполнение.
Для того, чтобы ускорить решение, необходимо заметить, что как только сосуд будет заполнен, то его можно выкинуть из рассмотрения во время выполнения процедуры наливания.
То есть вместо i = i + 1 присвоение должно выглядеть так i = найти_следующий_неполный_сосуд(i).
Для реализации этой функция существует множество структур данных. Например, можно использовать упорядоченное множество (set в C++, TreeSet в Java). Давайте поддерживать множество индексов незаполненных сосудов. Тогда для того, чтобы найти следующий сосуд после i-того необходимо найти наименьшее число в множестве, которое строго больше i. Для этого существуют встроенные методы (upper_bound в C++, higher в Java).
Так же, каждый раз, когда сосуд заполняется, соответствующий индекс необходимо удалять из множества.
Теперь алгоритм выполняет не более, чем O((m + n)logn) операций для всех запросов. Во время каждой итерации процедуры наливания существует два варианта: либо сосуд будет полностью заполнен водой (а такое может произойти только n раз, так как у нас всего n сосудов), либо у нас закончится вода и процедура завершится. Таким образом в сумме будет совершено не более, чем O(m + n) итераций процедуры наливания. Каждая итерация требует не более одного запроса к упорядоченному множеству, следовательно решение работает за O((m + n)logn).
371E - Реформа метро
Если внимательно изучить условие, то нетрудно увидеть, что наименьшее возможное среднее время фактически означает наименьшую сумму попарных расстояний между выбранными k станциями.
Сначала давайте отсортируем все станции по их координате. Главная идея в этой задаче заключается в том, что выбранные k станций обязательно будут следовать подряд в этом отсортированном списке. Ограничения не позволяют делать это “в лоб”, поэтому нам необходимо решение быстрее.
Определим функцию f(i, k) — попарное расстояние среди k подряд идущих в отсортированном списке станций, начиная с позиции i. Для начала, давайте подсчитаем f(0, k) (здесь и далее будем использовать 0-нумерацию). Это делается несложно за линейное время: по определению f(0, 0) = 0, а по значению f(0, i) найдем значение f(0, i + 1):
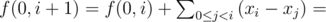
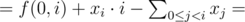
,
где функция sum(l, r) означает сумму xi, где l ≤ i ≤ r, значения этой функции легко считаются за O(1) с помощью частичных сумм.
Теперь научимся считать по значению f(i, k) значение f(i + 1, k): для этого необходимо исключить из набора координату xi и добавить xi + k. Аналогично выше рассуждениям: f(i + 1, k) = f(i, k) - (sum(i + 1, i + k - 1) - xi·(k - 1)) + (xi + k·(k - 1) - sum(i + 1, i + k - 1)).
Таким образом считаются значения f(i, k) для любых корректных значений i. Найдем минимальное значение, где оно достигается и выведем ответ. Решение работает за линейное время.











Тогда для того, чтобы найти следующий сосуд после i-того необходимо найти наименьшее число в множестве, которое строго больше i. Для этого существуют встроенные методы (upper_bound в C++, tailSet в Java).
В Java это все-таки называется higher
Вот еще одна опечатка, уже в 371С: вместо "Давайте для x подсчитаем, сколько будет стоит собрать эти гамбургеры." должно быть "Давайте для x подсчитаем, сколько будет стоитЬ собрать эти гамбургеры." А если еще немного почитать текст можно найти много лишних запятых перед "чтобы" и недостающие запятые после "таким образом". Не принимайте мой комментарий как упрек, а рассмотрите его как мое желание сделать разбор задач лучше:)
Если умничаешь по поводу русского языка, то хоть сам не делай ошибок ("много лишние запятые" -> "много лишних запятых").
in 371C, i have another way to solve it. first, we use nb, ns, nc as much as possible. then, we fill the rest if there are still somethings left and it may be used. finally, use the rest of the money to buy as much as possible. the time will not over O(max(nb,ns,nc)),and they are all not over 100.
You need to be careful to that the recipe doesn't use some kind of ingredients and its initial number is not 0. If you don't notice this case will get TLE. This solution 5390433 is my first submission and it doesn't check the case i describe.
yeah, i made the same mistake in my 1st submission toooo....
For 371E, we must pay attention to using LongLong instead of Int. I got an FST because of typing Int for numbers in my stucture. I will notice that in the following contests.
For 371E I used long long and got WA on test 11. Then I changed to unsigned long long and got AC.
in 371C please can anybody explain in detail how we can use binary search in this problem
you will calculate the number of bread,cheese and sauce needed for each recipe then you will try to maximize your solution which can be affordable using binary search
BFS solution for 371B.. :) http://codeforces.net/contest/371/submission/16594018
In the question E, can’t we just find the shortest segment containing k numbers after sorting? I tried that and am getting wrong answer. What I thought was if the distance between the two ends is shortest, the pairwise sum of absolute distance of the points in between will also be minimum...
Can anyone give an example where this goes wrong?
try this n=4 1 3 5 7 n=4 1 5 6 7 Both will give different pairwise distance.
Find error if possible. https://codeforces.net/contest/371/submission/43155192
In problem B, how did he derive the forms of the two numbers?? what formula/theories he used?
We can just repeatedly divide by 2 first, then 3 and then 5 to find a2, a3, a5. If after division, both numbers aren't equal => there is no solution and you can return -1. Else, you return abs(a2 — b2) + abs(a3 — b3) + abs(a5 — b5).
Here is my code: https://codeforces.net/problemset/submission/371/52334277
I think It is not a good a good editorial. You should also give the code too. There are many people like me who needs the code as well as explanation to understand the editorial clearly. Please consider giving implementation in editorial.
If you need the code, you can view other people's submissions. Sorting by execution time can give you the most optimal ones.
But I need code that is the implementation of the idea given in Editorial. In people's submission I will not have it. Don't you think implementation should be given in editorial ?
Yeah, it would definitely be better if it was given in the editorial, but if not hopefully someone else has solved it in the same way.
For D, solution using Disjoint Sets.
in 371C, in this case, BBBBBBBBBBCCCCCCCCCCCCCCCCCCCCSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS 10 20 40 100 100 100 300 the given answer is 0 but he can make 1 hamburger right ? as nb, nc, ns are equal to the required count of b, s, and c.
How did you figure out the value of "high" is 1e13?